医療現場で取得するデータには、欠測値(もしくは欠損値)の発生がつきものです。
欠測をそのままにして解析すると、バイアスが生じてしまう可能性があります。
そのため、欠測に対しては適切に対処しなければならないです。
欠測を補完する代表的な方法が多重代入法です。
この記事では、多重代入法を SPSS で行う方法について解説してきます。
多重代入法とは
多重代入法とは、本当はデータがあるはずなのに、何かの事情でデータが得られなかった、欠測値(けっそくち)(欠損値 けっそんち とも言う)を、適切な数値で埋める(代入する・補完する)ことを言います。
多重代入の多重とは、いくつかの値を代入した、いくつかのデータセットを作るという意味です。
いくつかと言っても決して少なくない数で、100 ~ 1000 のデータセットを作るのが良いと言われています。
欠測しているデータの真実はわからないため、いくつかの値で代入したデータセットを作成し、最終的に結果を統合して、バイアスが少ないと考えられる結果としてまとめる方法と言えます。
では、どのように代入するかというと、欠測した変数の値を、測定できている値から推測して、代入するのです。
連続データと二値カテゴリカルデータでは、方法が異なります。
連続データの場合は、重回帰分析を用いて予測モデルを作成して、その予測値と近い値を代入する PMM(予測平均マッチング)という方法を用います。
二値カテゴリカルデータの場合は、ロジスティック回帰分析を用いて予測値を求めて、代入します。
詳しくは、以下の論文をご覧ください。
多重代入法のステップ
多重代入法は、3 つのステップからなります。
- 代入する値の生成と複数の代入データセットの作成
- 多重代入データセットを用いた解析
- 複数のデータセットから得られた結果の統合
詳しくは、以下の記事もご覧ください。
多重代入法(多重補完法)をわかりやすく解説!EZRでは実施できる?
以下では、SPSS で、これらのステップを行う方法を解説します。
多重代入法を SPSS で行うための準備
SPSS で多重代入法を行うには、Complex SamplingおよびTesting と呼ばれるアドオンが必要です。
まだ、購入していない場合は、追加購入する必要があります。
詳しくはこちらをご覧ください。
アドオンが導入されると、「分析」メニューに「多重代入」が追加されます。
分析 → 多重代入 → 欠損データ値を代入 から多重代入を実施していきます。
多重代入法を SPSS で行う方法
「欠損データ値を代入」メニューの設定方法
分析 → 多重代入 → 欠損データ値を代入 メニューを選択すると、以下のウインドが開きます。
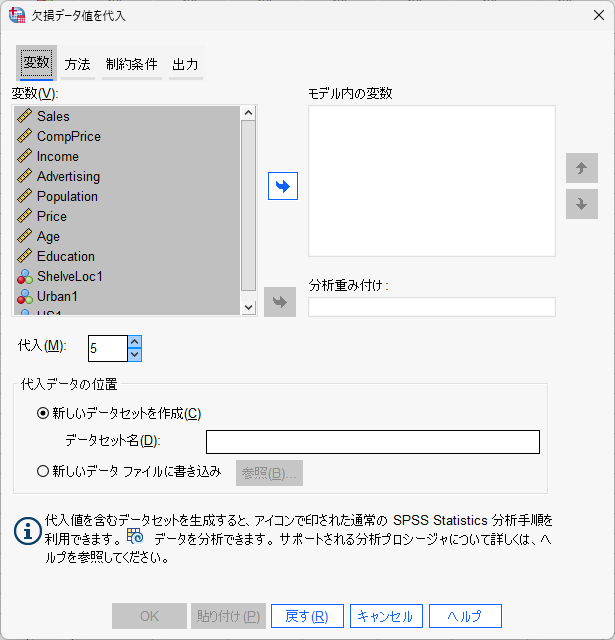
変数タブの設定
「変数」枠から多重代入に用いるデータを「モデル内の変数」に投入します。
変数同士を足し合わせて計算する合計値などは投入せず、多重代入後のデータセット上で、変換メニューから計算して補完します。
また、このとき目的変数も投入します。
代入数は、100 ~ 1000 の最低数として 100 としておきましょう。
任意の新しいデータセット名を書き入れます。
設定すると、以下のようになります。
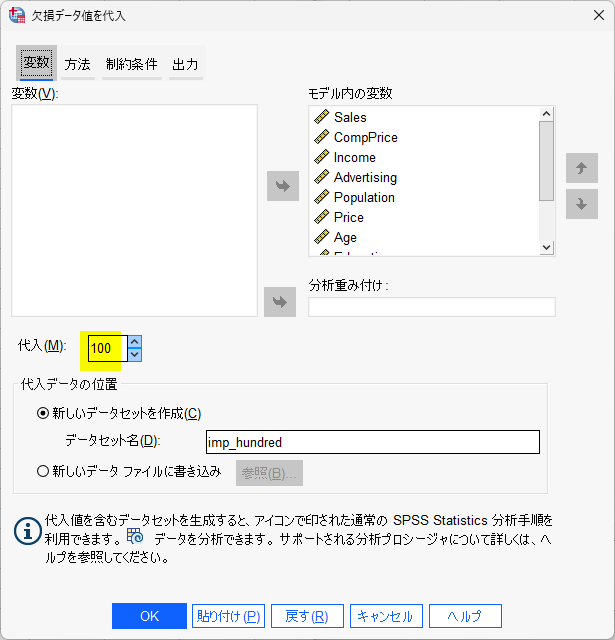
方法タブの設定
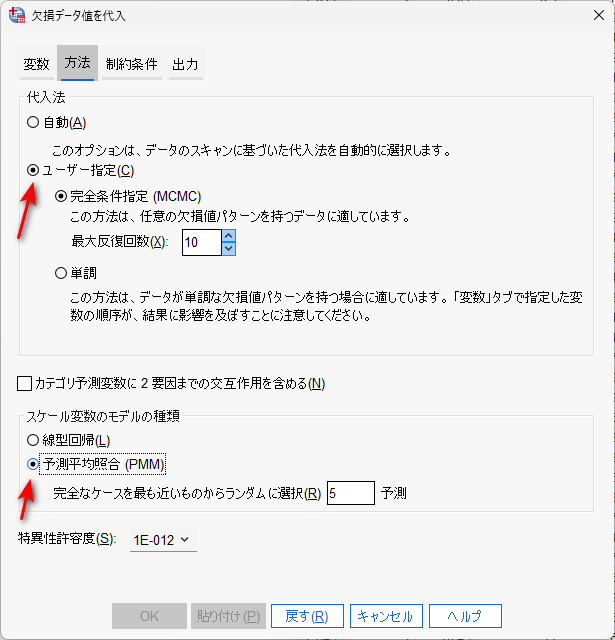
方法タブは、多重代入の方法を指定するタブです。
方法タブを開き、代入法の枠内の「ユーザー指定」を選択します。
また、スケール変数のモデルの種類枠の「予測平均照合(PMM)」を選択します。
これで、方法タブの設定は OK です。
制約条件タブ
制約条件とは、補完する値の上限や下限を決めるという意味です。
例えば、5 件法のアンケート回答の欠測を補完したい場合、1 から 5 の値が代入されてほしいところ、0 や 6 が代入されてしまうことがあり、そのような想定外の代入を避けるために条件を設定できるわけです。
特に制約が必要なければ、設定不要です。
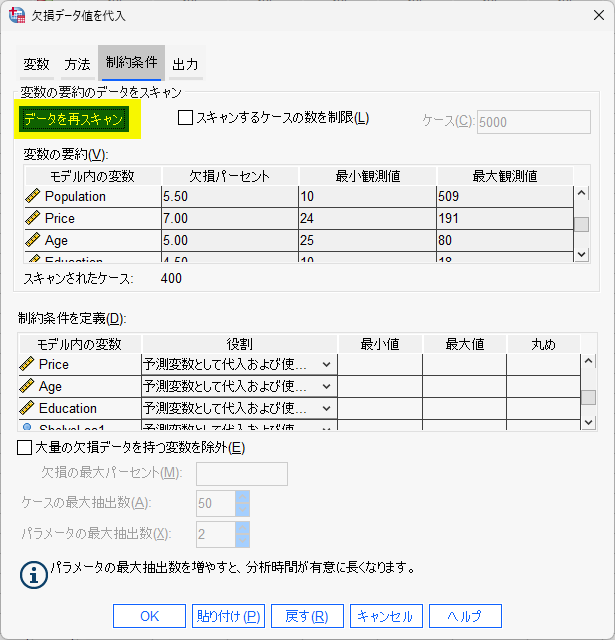
「データをスキャン」とクリックすると、「変数の要約」と「制約条件を定義」に情報が反映されます。
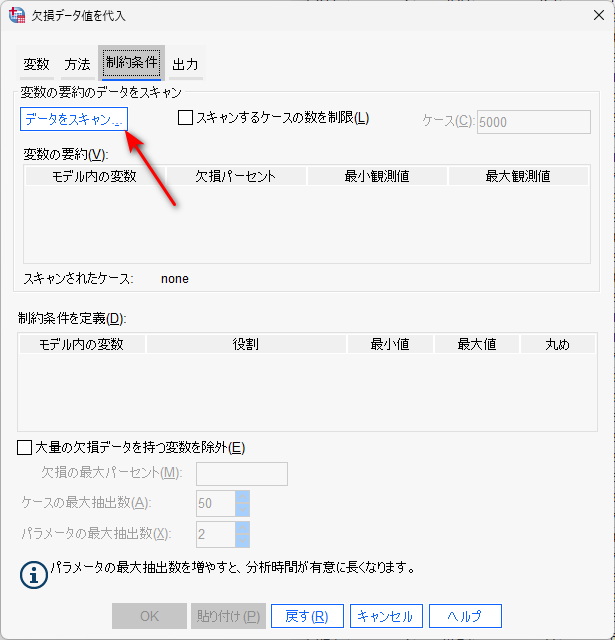
変数の要約欄では、欠測値の割合、最小・最大の観測値が示されます。
制約条件を定義欄で、予測に使って代入もするか、予測だけに使うか、代入だけするか、を決めたり、最小値・最大値を決めたりできます。
「データを再スキャン」をクリックすると、再度スキャンを実行してくれます。
出力タブ
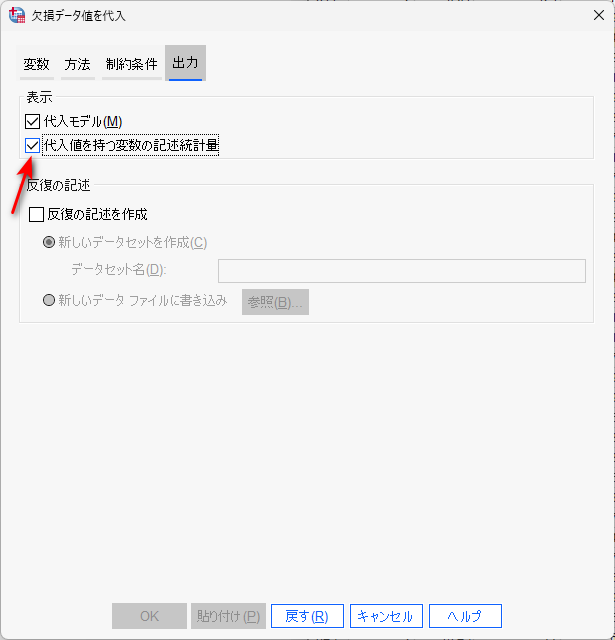
出力タブは、多重代入を行った後に、どんな出力をするかを設定できるタブです。
デフォルトでは、どんな変数を用いた代入モデル(PMM や ロジスティック回帰)が使われたかの詳細が出力されます。
追加で「代入値を持つ変数の記述統計量」を出力しておけば、欠測が代入されたデータセットの記述統計を確認することができます。
設定が済んだら、OK をクリックすると、多重代入が行われて、変数タブで指定した代入数だけ、データセットが作成されます。
多重代入後のデータセット
それでは、多重代入後のデータセットをデータビューで見てみましょう。
まず、左端に Imputation_ という変数が作成されています。
0 が元のデータで、1 以上が、代入したデータを意味しています。
右上には、どのデータを選択するかのドロップダウンリストが見えます。
.png)
元のデータは、セル内に「.」が入っている欠測があるのが見て取れます。
右上のドロップダウンリストから代入データセットを選ぶことができます。
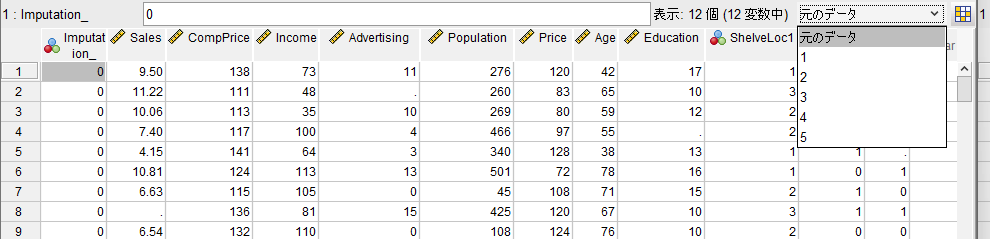
代入された、元欠測データ箇所は、うすい黄色でハイライトされています。
.png)
ここでは示しませんが、ほかのデータセットと見比べてみると、異なる値が代入されていることがわかります。
一つ気を付けたいのは、この多重代入は再現性を保つ方法がありません。
下の図の左右は、同じ欠測データを用いて、2 回多重代入を行った結果の比較です。
.png)
同じ代入データセット番号(Imputation_ 番号)ですが、異なった代入値になっているのがわかると思います。
なので、一度作成した多重代入データセットは、必ず保存するようにしましょう。
解析結果だけ保存して、データセットを保存しなかった場合、同じ解析結果が得られる、同じ多重代入データセットを、再度作成することはできません。
また、保存した多重代入データセットを一度閉じた後、再度開くと以下のメッセージが出力されます。

これは、Imputation_ でデータの分割を実行することで、再び多重代入データセットであることを認識させて下さい、という意味です。
認識させる方法は、データ → ファイルの分割 メニューを選んで、Imputation_ をグループ化変数として、グループの比較を行うように設定します。
.png)
さらに、右上に「元データ」と見えるドロップダウンリストが表示されていなければ、”キラキラボタン”(と勝手に呼んでいる)ボタンをクリックします。
このように設定すると、多重代入後の解析・統合の作業が再開できます。
このセクションの締めくくりとして、多重代入データセットができるのと同時に、出力される結果を説明します。
代入モデルに関しては、以下のように出力され、どの方法で、どの変数を使ったモデルで代入したかの記録が残ります。
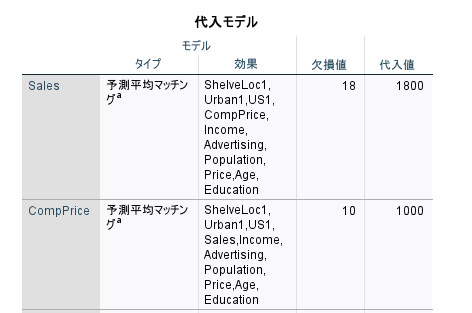
また、代入した変数の記述統計は以下のように出力されます。代入データセットが 100 の場合は、100 行、出力されます。
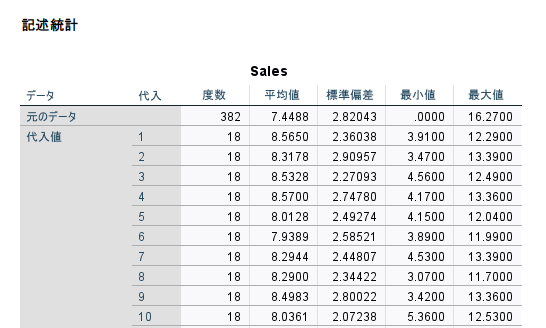
代入されている値が、元のデータ(欠測以外)と比較して、少しずれているのがわかります。
代入方法の計算上、少しずれている値のほうがよいと判断されて代入されていると考えればよいです。
多重代入後の解析例
それでは、多重代入データセットができたところで、そのデータセットを使った解析・統合の方法を、2 群・多群の平均値・割合及び回帰モデル別に解説します。
T 検定(2 群の平均値の差の検定)
T 検定は、分析 → 平均値と比率の比較 → 独立したサンプルの t 検定 メニューで分析できます。
独立したサンプルの t 検定のアイコンにうずまきがついていれば、解析・統合できる状態を表しています。

もし、うずまきマークが出ていないようであれば、データセット右上の “キラキラボタン” をクリックして、「元データ」とあるドロップダウンリストを表示させてから、再度、独立したサンプルの t 検定 メニューまで行ってください。
そうすると、うずまきマークが出ていると思います。
T 検定の設定は、通常のデータセットのときと同じです。
例えば、以下のように、連続データを検定変数に、カテゴリカルデータをグループ化変数に、それぞれ投入し、グループの定義も設定します。
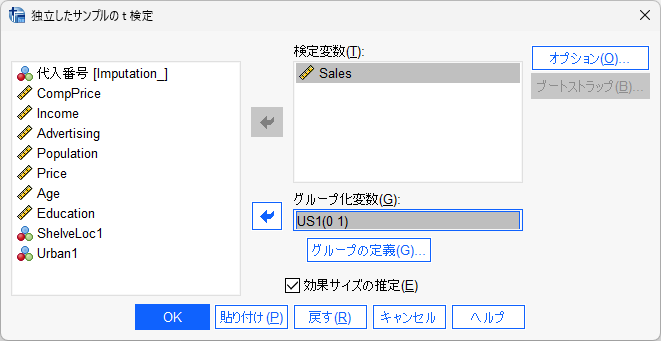
OK をクリックすれば、結果が計算されます。
まずは、グループ統計量を見ます。
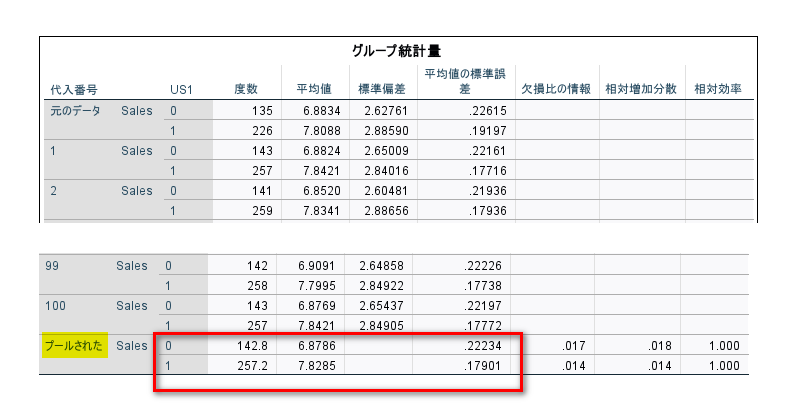
「プールされた」のところを見ると、度数に小数点があるのがわかります。
これは、グループ変数 US1 も多重代入しているからです。
グループ変数は代入しないことにすれば、小数点は生じません。
そして、レポートする数値としては、平均値と平均値の標準誤差が良いと思います。
検定結果は、「独立サンプルの検定」表を参照します。
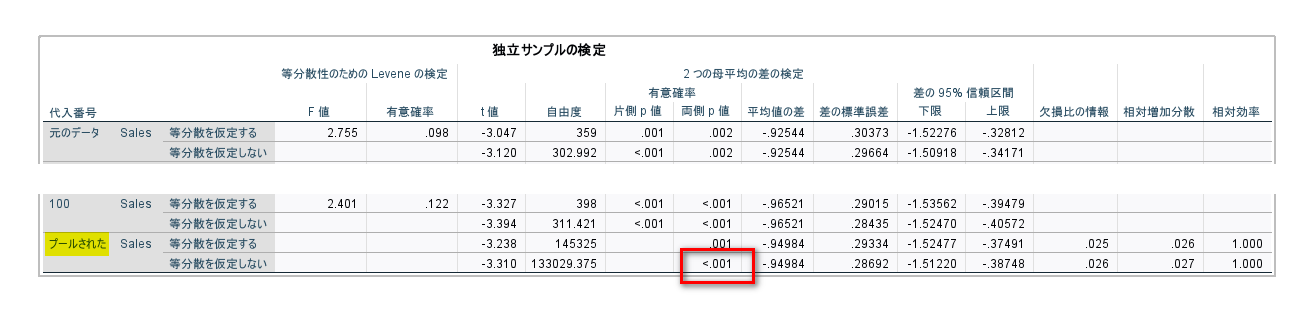
「プールされた」の欄の等分散を仮定しない結果の両側 P 値を報告するとよいでしょう。
一元配置分散分析・多重比較(3 群)
一元配置分散分析、もしくは、連続データの多重比較の場合は、分析 → 平均値と比率の比較 → 一元配置分散分析と進みます。
一元配置分散分析のアイコンにうずまきがついていれば、分析・統合可能の印です。
一元配置分散分析では、例えば以下のように変数を設定します。
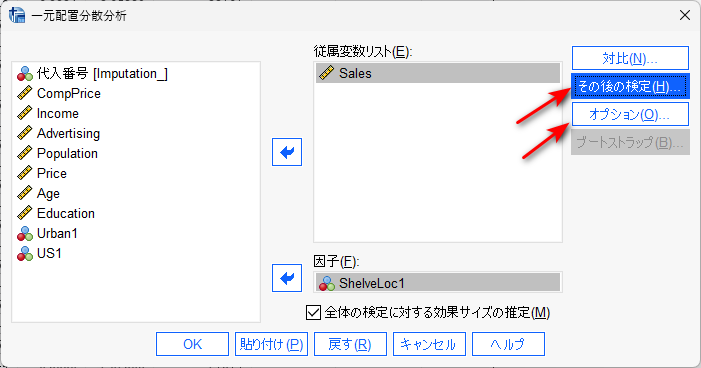
従属変数リストに、連続データを投入し、因子に、カテゴリカルデータを投入します。
オプションボタンをクリックして、記述統計量を出力させるようにチェックを入れます。
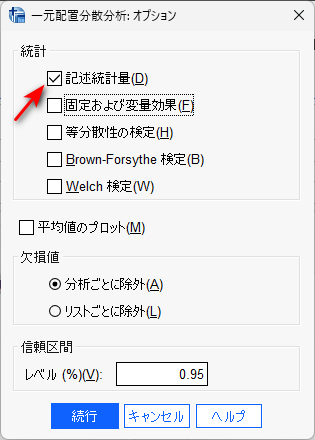
多重比較は、その後の検定ボタンをクリックして、LSD(多重比較調整なし)を設定します。必要に応じて、多重比較調整手法(例:Bonferroni)を選びます。
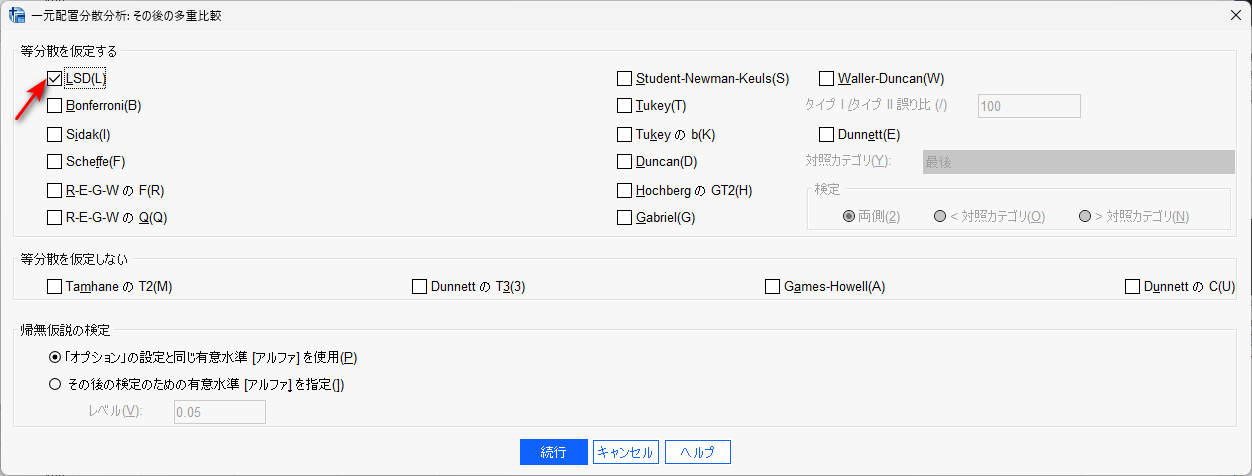
続行をクリックして戻り、OK をクリックすると分析結果が出力されます。
記述統計の表の最下段に、「プールされた」結果が出力されています。
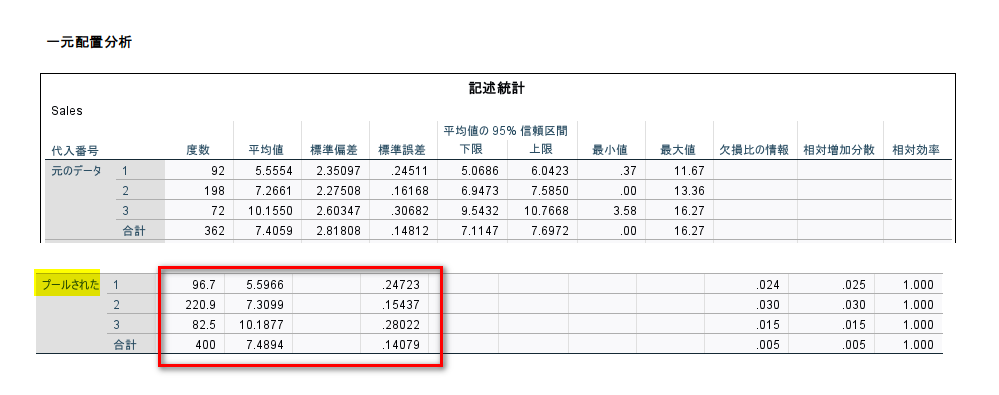
ですが、検定結果は、「プールされた」が表示されず、統合された結果は得られません。
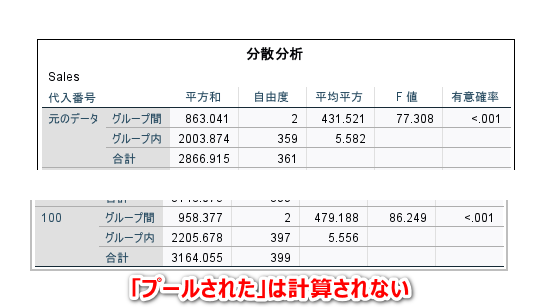
多重比較の結果も、「プールされた」が計算されません。
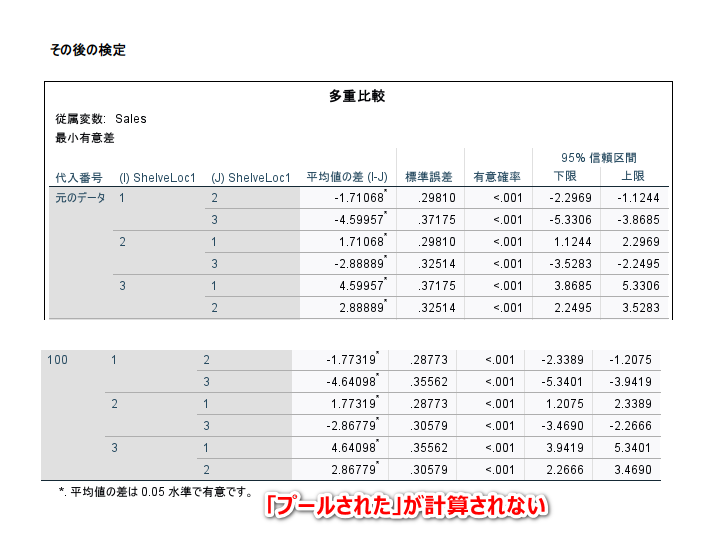
よって、3 群以上の平均値を比較した検定結果が欲しい場合は、下記に示す共分散分析の方法に従って、従属変数の連続データと固定因子を投入し、共変量を入れない形で、実施するのが良いと思います。
カイ二乗検定(2 x 2 分割表)
2 群のカテゴリカルデータを比較するときのカイ二乗検定は、分析 → 記述統計 → クロス集計表 と進んで実行します。
クロス集計表の先頭のアイコンにうずまきがついていれば、分析・統合可能の合図です。
クロス集計表の設定は、例えば、以下のようにします。
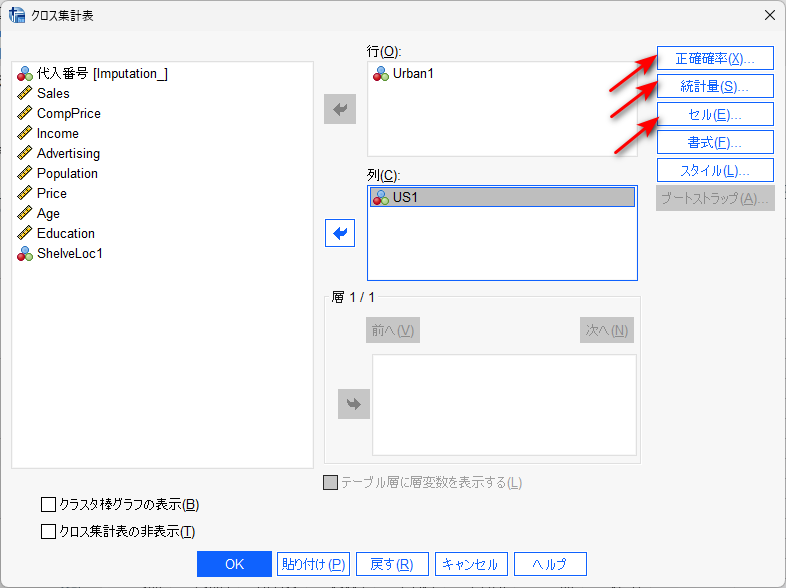
行にも、列にも、2 値のカテゴリカルデータを投入します。
正規確率ボタンをクリックして、「正確」のボタンをクリックします。
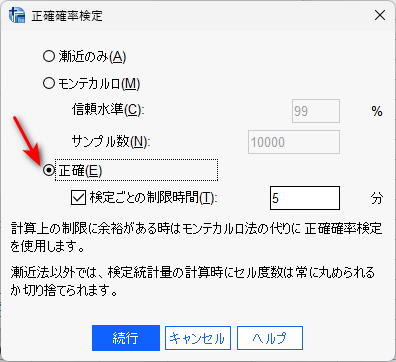
統計量ボタンをクリックして、カイ2乗にチェックを入れます。
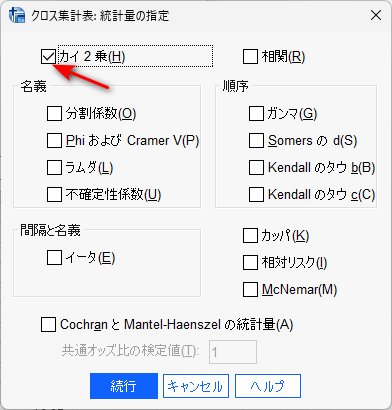
セルボタンをクリックして、列パーセンテージにチェックを入れます。
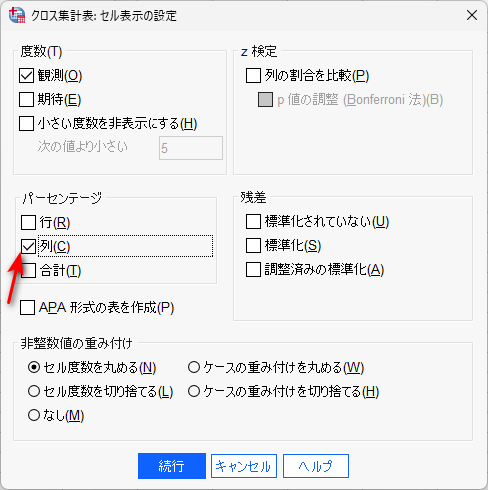
続行で戻り、OK をクリックすると、解析結果が出力されます。
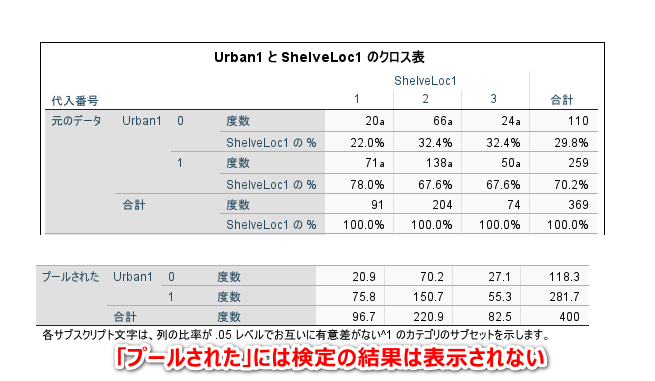
クロス表の最下段を見ると、統合された度数が表示されていますが、パーセンテージは統合されないことがわかります。
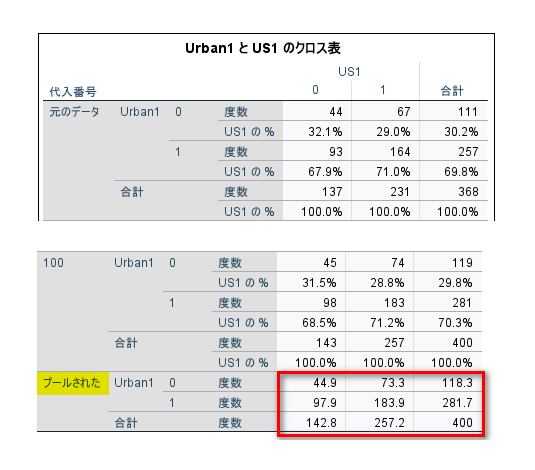
カイ2乗検定の表の最下段を見ると、検定結果も統合されないことがわかります。
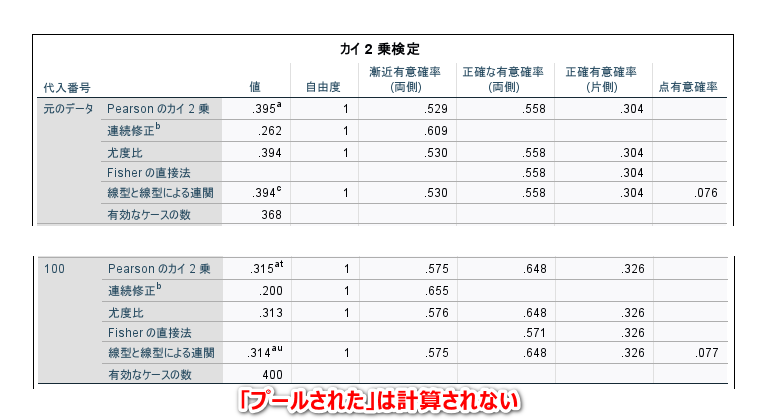
ですので、検定結果が欲しい場合は、下記に示す、二項ロジスティックのメニューで、共変量にカテゴリカルデータを 1 つだけ投入した、単変量解析をするのが良いと思います。
カイ二乗検定・多重比較(2 x 3 分割表)
2 値のカテゴリカルデータを 3 群やそれ以上で比較したい場合も、同じく 分析 → 記述統計 → クロス集計表メニューを使います。
行と列の設定は、上記 2×2 と同様です。
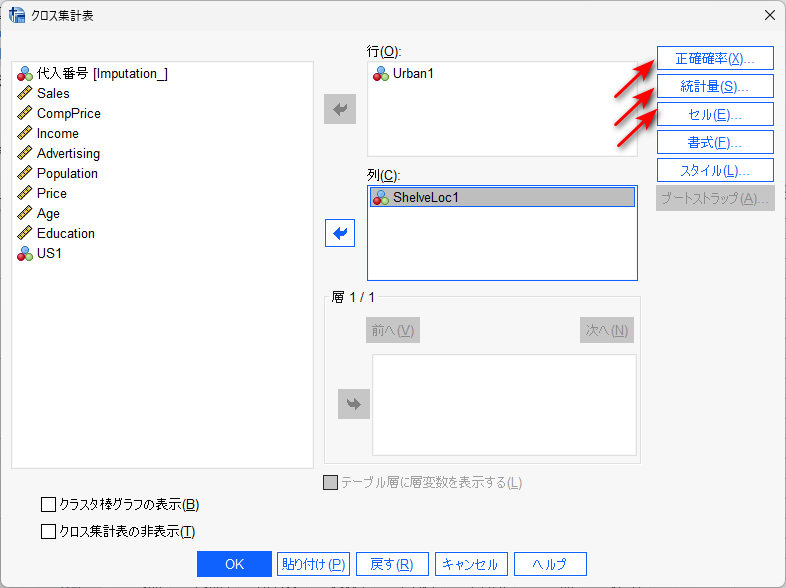
正確確率と統計量の設定は、上記 2×2 の場合と同じです。
セルの設定は、以下のように、列パーセンテージのほかに、z 検定にチェックを入れます。
z 検定は、この場合、多重比較の検定です。
必要に応じて、p 値の調整(Bonferroni 法)にもチェックを入れます。
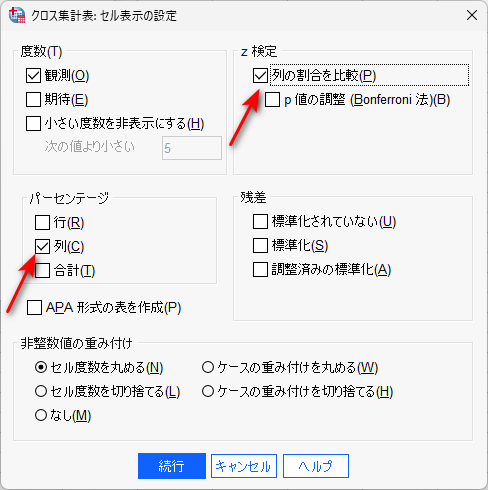
続行をクリックして戻り、OK をクリックすると解析結果が出力されます。
クロス表の「プールされた」のところは、多重比較の検定結果は表示されておらず、統合した多重比較検定結果は得られません。
カイ2乗検定の表では、「プールされた」がなく、検定結果は統合されません。
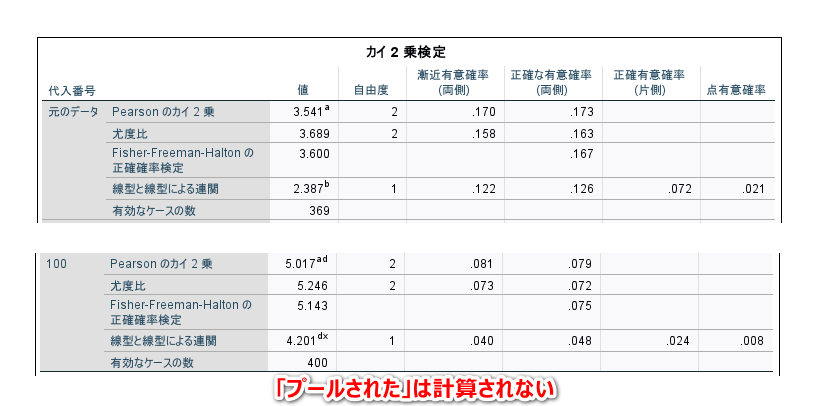
したがって、こちらも、検定結果が欲しい場合は、二項ロジスティックのメニューで、共変量に 3 群のカテゴリカルデータを投入し、カテゴリ変数と認識させたうえで、単変量解析を行うのが良いと思います。
重回帰分析(すべての説明変数が連続データの重回帰分析)
すべての説明変数が連続データの場合の重回帰分析の方法です。
分析 → 回帰 → 線型 メニューで解析できます。
ここで、「線型」とあるところの先頭のアイコンにうずまきマークが出ていれば、多重代入データセットを使って解析・統合できる状態であることを意味しています。
重回帰分析の設定は通常のデータセットの時と同様です。
例えば、以下のように目的変数(従属変数)と説明変数(独立変数)を投入します。
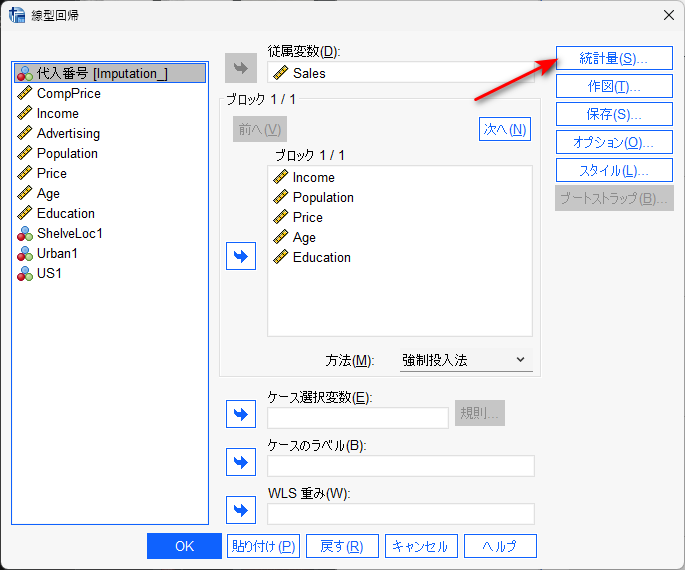
統計量ボタンをクリックして、信頼区間にチェックを入れます。
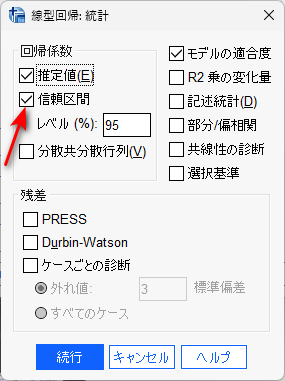
続行で戻り、OK をクリックすると、解析結果が得られます。
係数というタイトルの表がメインの結果となります。
一番下の「プールされた」とあるセクションの値が、多重代入データセットの解析結果を統合した報告すべき結果となります。
具体的には、赤枠内を報告するのが良いと思います(標準誤差と t 値は割愛可能)
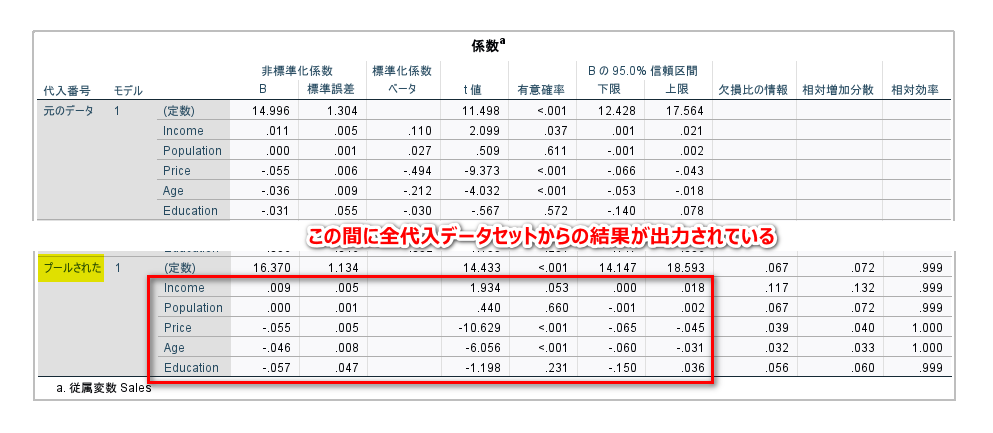
標準化係数ベータ(標準化偏回帰係数)は、統合できず、結果は表示されません。
共分散分析(群間比較を共変量で調整する重回帰分析)
群の背景情報を共変量として調整した平均値比較を行うための重回帰分析のことを、共分散分析とも言います。
SPSS で、共分散分析を行うには、分析 → 一般線型モデル → 1 変量 メニューを使います。
SPSS で共分散分析を行う方法は、以下の記事も参考にしてください。
共分散分析をSPSSで実施!多変量解析(重回帰分析)はどう判断する?
1 変量メニューのアイコンにうずまきが付いていれば、多重代入データセットの解析・統合の準備ができています。
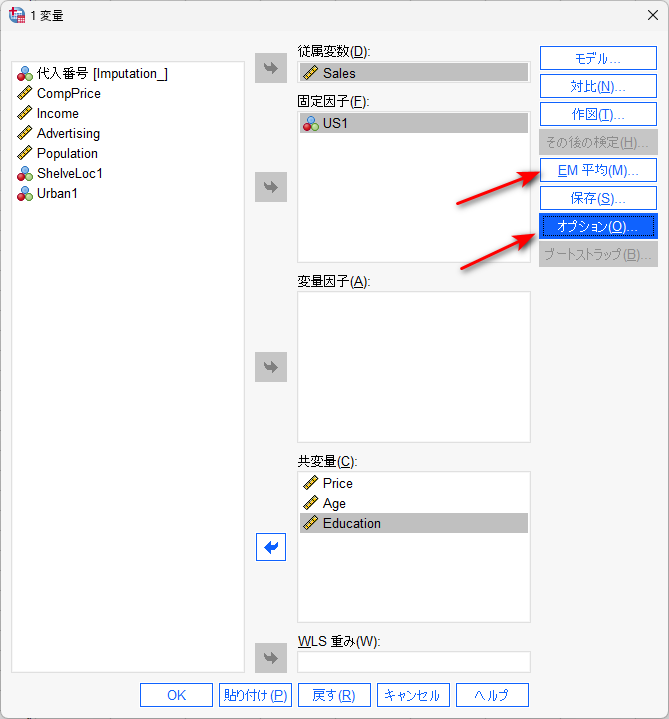
解析のための設定は、例えば以下のように変数を投入します。
群間比較のためのカテゴリカルデータは、固定因子枠に投入します。
この時、固定因子のみ投入し、共変量を投入しなければ、従属変数の固定因子カテゴリ間比較になります。
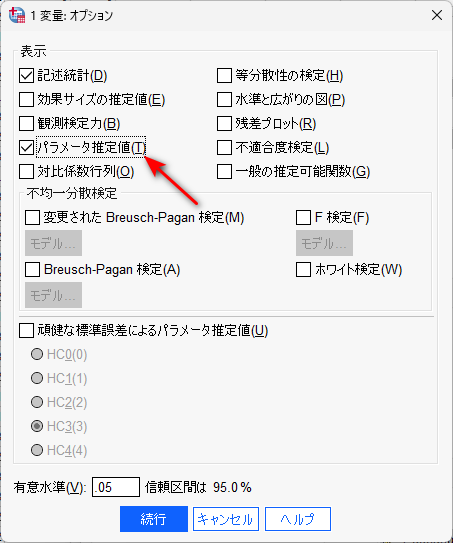
オプションボタンをクリックして、パラメータ推定値が出力されるようにします。
記述統計にもチェックを付けて、確認しておくとよいでしょう。
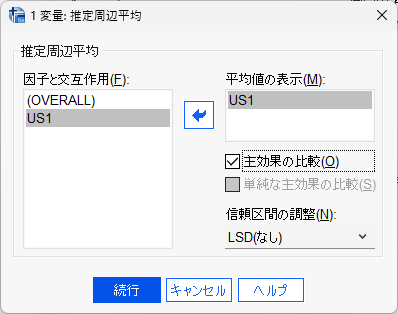
固定因子の群間比較は、EM(Estimated Marginal 推定周辺)平均ボタンをクリックして、例えば、以下のように設定します。
結果は、パラメータ推定値の表と、推定周辺平均の推定値とペアごとの比較を見ます。
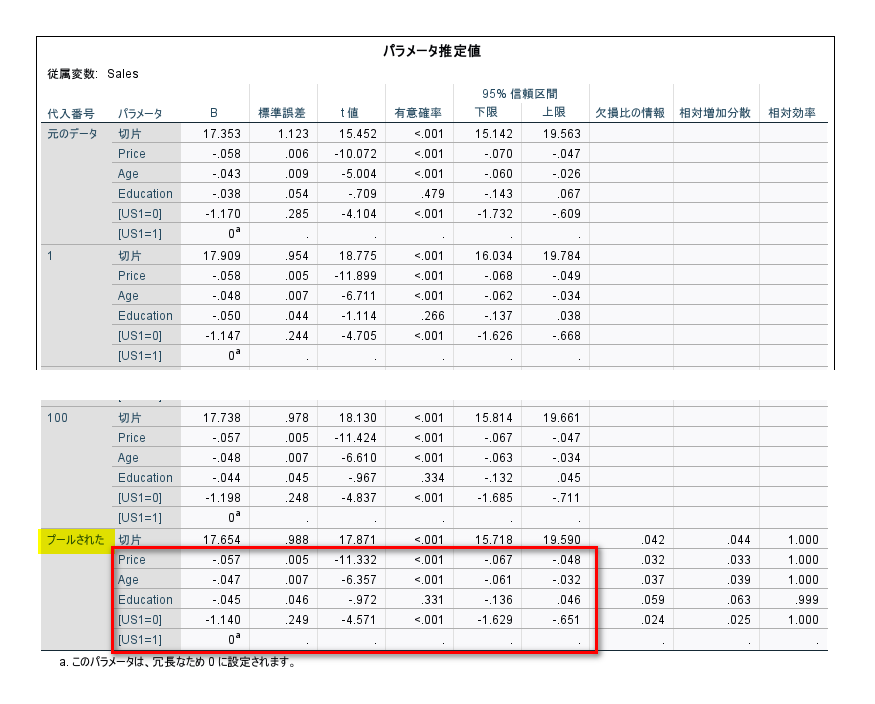
パラメータ推定値の表では、各説明変数のB=パラメータ推定値=偏回帰係数及び群間の検定結果が確認できます。
代入番号「プールされた」の赤枠部分を報告するのが良いと思います。
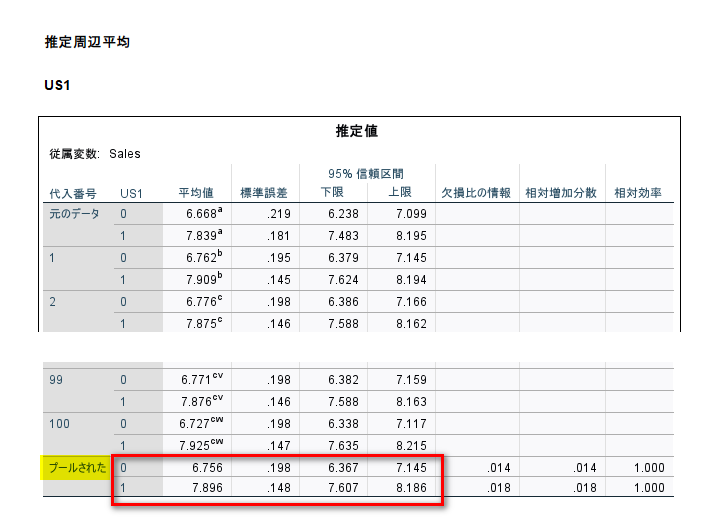
推定周辺平均の推定値は、共分散分析を行った重回帰モデル(一般線型モデルとも呼ばれます)から推定された、交絡因子調整をした後の群ごとの平均値(調整平均)です。
推定値の表のうち、代入番号が「プールされた」の赤枠の部分が、統合された結果で、この数値を報告するのが良いと思います。
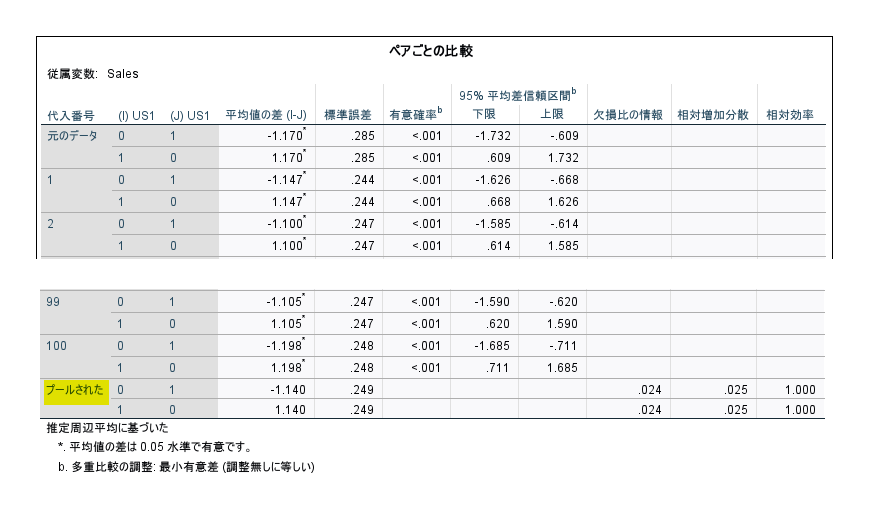
ペアごとの比較表も、代入番号「プールされた」の場所を見ます。
ですが、パラメータ推定値表とは違って、比較検定結果は統合できず、統合結果は表示されません。
検定結果は、上記のパラメータ推定値表の結果を使うのが良いと思います。
ロジスティック回帰分析
ロジスティック回帰分析の場合、分析 → 回帰 → 二項ロジスティック メニューで解析します。
SPSS でロジスティック回帰を行う方法は、以下も参考にしてください。
SPSSで多重ロジスティック回帰分析をわかりやすく!結果の見方や解釈まで
二項ロジスティックの先頭アイコンにうずまきがついていれば、多重代入データセットを解析して統合する準備が完了しています。
解析自体は、通常のデータセットでロジスティック回帰分析を行うときと同じです。
例えば、以下のように変数をセットします。
この時、共変量にカテゴリカルデータ一つだけを入れれば、従属変数のカテゴリ間比較になります。
カテゴリボタンで、共変量のうち、カテゴリカルデータである変数を指定します。
オプションボタンで、95 % 信頼区間を表示させる指定をします。
続行で戻り、OK をクリックすると、解析結果が出力されます。
ブロック 1:強制投入法の「方程式中の変数」表を確認します。
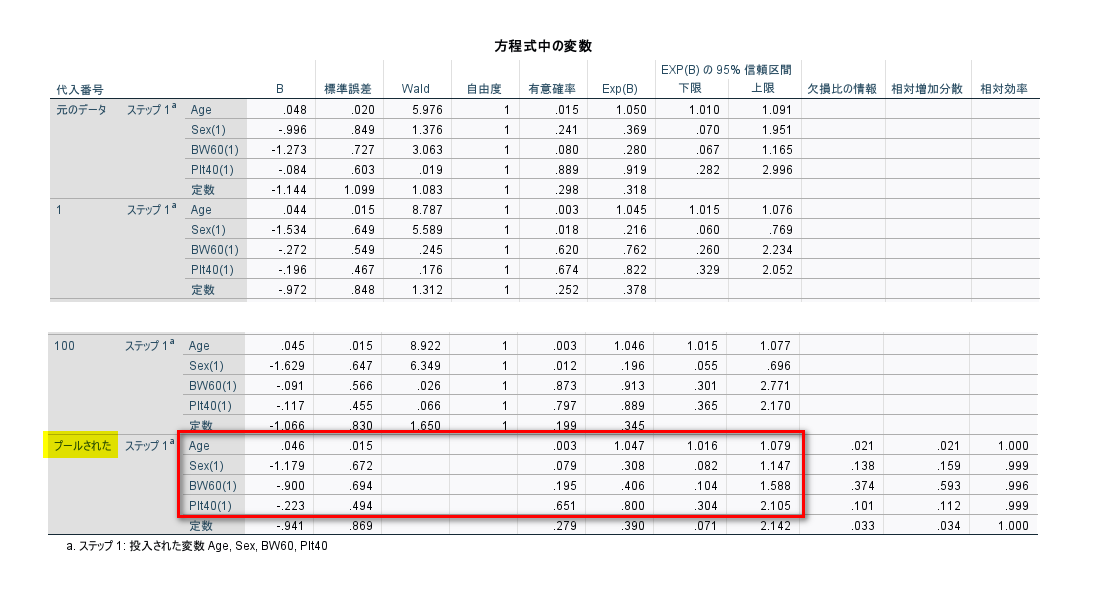
代入番号「プールされた」の赤枠部分が報告する結果です(B=パラメータ推定値=偏回帰係数=対数オッズ比、標準誤差は割愛可能)
Cox 比例ハザードモデル
Cox 比例ハザードモデルの場合、分析 → 生存分析 → Cox 回帰 メニューで解析します。
SPSS で Cox 回帰を実施する方法は、以下も参考にしてください。
SPSSで3群のCox回帰を実施!3群間の比較は結果の解釈に注意
Cox 回帰の先頭アイコンにうずまきがついていれば、多重代入データセットを解析して統合できる準備ができています。
解析自体は、通常のデータセットで、Cox 回帰するときと同じです。
例えば、以下のように設定します。
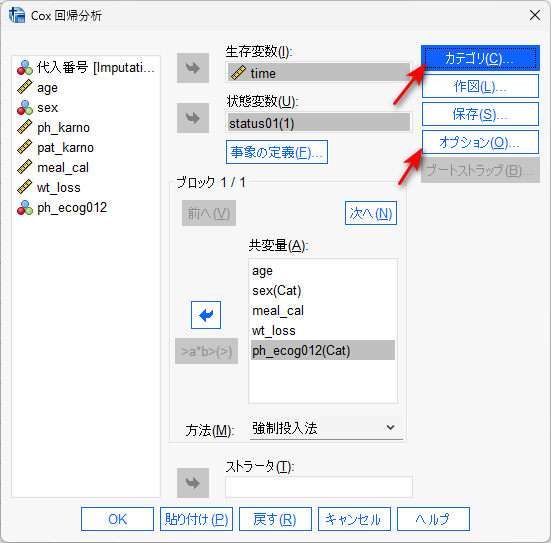
カテゴリカルデータは、カテゴリボタンをクリックして、カテゴリカル変数であることを認識させます。
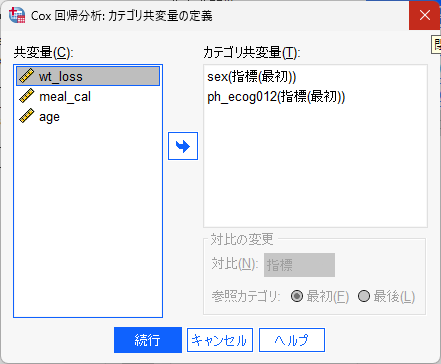
オプションボタンをクリックして、95 % 信頼区間を出力するように指定します。
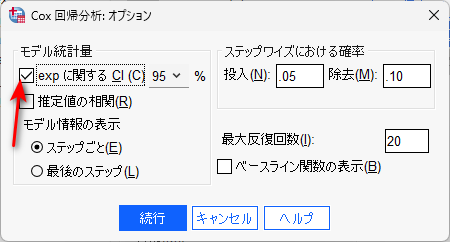
続行をクリックして戻り、OK をクリックすると、解析が実行されます。
解析結果は、「方程式中の変数」表を見ます。
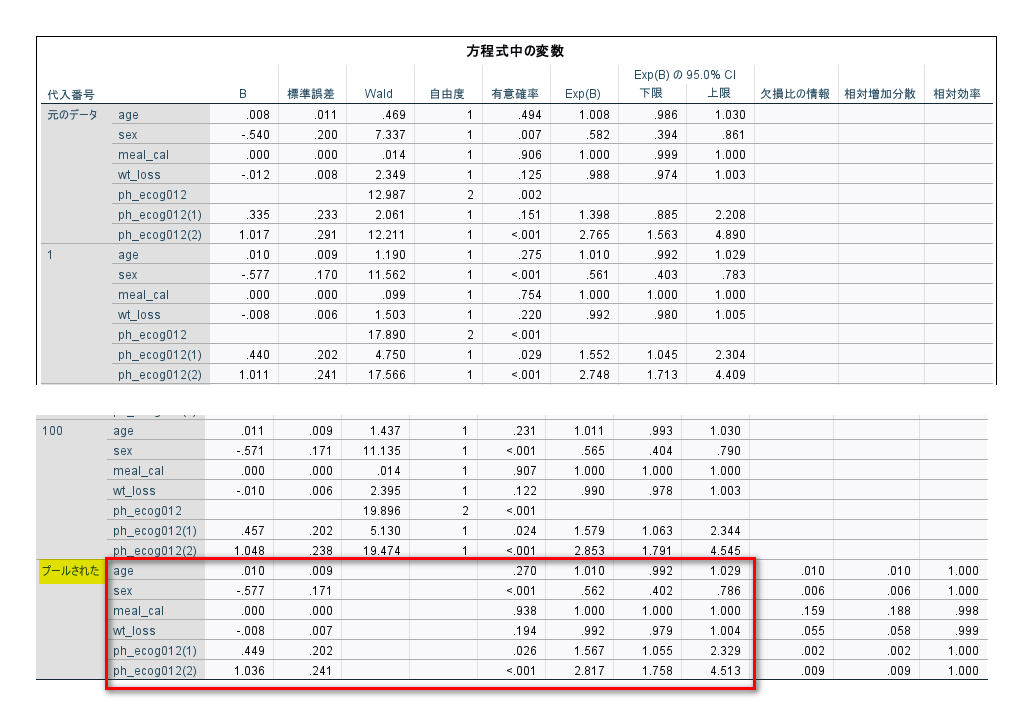
一番下の「プールされた」という部分の数値の赤枠部分が報告する結果になります。
まとめ
以上、SPSS で多重代入法を行う方法を解説しました。
多重代入法は、3 つのステップからなります
- 代入する値の生成と複数の代入データセットの作成
- 多重代入データセットを用いた解析
- 複数のデータセットから得られた結果の統合
の 3 ステップです。
多重代入データセット作成について、連続データは PMM(予測平均マッチング)で行い、少なくとも 100 個は作りましょう。
連続データの 2 群比較は、T 検定で行えます。
一方、連続データの 3 群以上の比較、カテゴリカルデータの 2 群比較、3 群以上比較は、いずれも、検定結果が統合できないため、それぞれ、一般線型モデル → 1 変量メニュー、二項ロジスティックメニューを使いましょう。
重回帰分析、共分散分析、ロジスティック回帰、Cox 回帰のそれぞれの方法を解説しました。
参考になれば幸いです。












コメント