この記事では「多重代入法（多重補完法）をわかりやすく解説！EZRでは実施できる？」ということでお伝えします。
多重代入法（Multiple Imputation）は、医療系の論文でよく使われる方法。
ですが「どういった目的で使われて、実際にどうすればいいの？」と思われるかもしれません。
そのため
- 多重代入法とは欠測値（欠損値）に対応する方法である
- 多重代入法の概念をわかりやすく解説
- EZRで多重代入法はできる？
ということをわかりやすく解説します！
Contents
多重代入法とは欠測値（欠損値）に対応する方法
そもそも欠測値とは、本来得られるはずだったデータが得られていないことです。
例えば、下記のようなデータの黄色いセル。
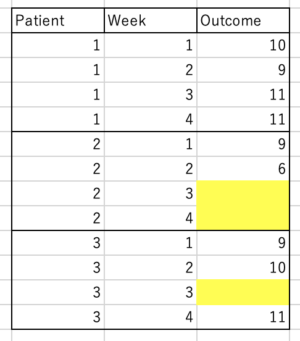
全被験者からWeek4までデータを取りたかったのですが、被験者2ではWeek3とWeek4のデータが取られていません。
同様に、被験者3ではWeek3のデータが取られていません。
こういったデータのことを欠測値（欠損値）と呼んでいます。
欠測値があると何が問題なのか？
では、欠測値があると何が問題になるのでしょうか？
大きく分けると3つあります。
- 本来得られるはずだった解析結果が得られにくくなる
- データ数が少なくなる
- 試験の信頼性の問題になる
欠測値は「本来得られるはずだったデータが得られていない」ことですから、欠測のあるデータ全体で解析をしても、本来得たかった解析結果は得られにくいですよね。
そもそも欠測値をそのまま放置して解析をするとデータ数が少なくなるため、サンプルサイズの小ささにつながります。
また、多少の欠測はどの研究でもあり得るとは認識されていますが、欠測が多すぎるとその試験自体「大丈夫か！？」となってしまいます。
そのため、どれだけ欠測値への対処が適切でも、欠測値が多すぎれば意味がないことに。
なので大前提としては大前提として欠測を起こさないことが大事であることは念頭に置いておきましょう。
欠測値への対処方法は？
では欠測値が発生したとして、対処法や埋め方（補完方法）はあるのでしょうか？
大きく分けると3つほどあります。
- 単一補完（Single Imputation）
- 多重補完（Multiple Imputation）
- モデル解析（一般化線形混合モデル：Generalized Linear Mixed Model）
詳しくは「欠測値（欠損値）とは？埋め方（補完方法）や対処法はある？」という記事を見ていただきたいですが、最近の傾向では多重補完かモデル解析がいいとされています。
しかし、どんな方法でも「これがベスト」という方法はないことは前提であると理解しておきましょう。
なぜなら欠測じゃなかった時にどんな値だったか誰も知らないから。
欠測への対処方法には、強い仮定が入ります。
そのため、仮定をずらしても同じ解析結果が得られるのか、という感度解析を実施することがとても重要。
感度解析として実施した複数の解析で結論が同じになれば、例え欠測があったとしても頑健性のあるデータだったということを主張できます。
多重代入法の概念をわかりやすく解説
欠測値が何かを理解できたところで、多重代入法（Multiple Imputation）について解説していきます。
多重代入法の手順は、下記の4つ。
- 観測されているデータを基にして欠測データの事後分布を構築し、この事後分布からの無作為抽出を行って欠測を埋める。
- 1の手順で無作為に欠測を埋めたデータセットをM個（＞1）用意する。
- M個のデータセットそれぞれに対して解析を実施する（M個の結果が得られる）
- M個の結果を適切な統合方法で1つに統合する（最終的に1つの結果が得られる）
この手順のイメージは、高橋先生・伊藤先生のこちらの論文の図2.1がわかりやすいです。
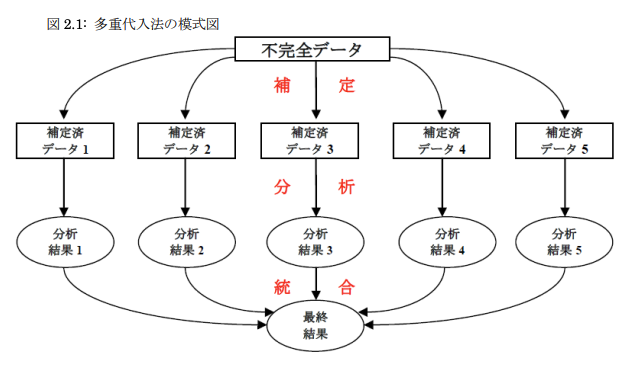
重要なのは「M個のデータセットそれぞれに対して解析を実施し、最後に統合する」という手順。
M個のデータセットの平均を計算して1つのデータセットにして1回の解析をする、という間違った手順で理解している方がいるので注意が必要です。
多重代入法では何個のデータセット作成が必要？
多重代入法としてM個のデータセットを作って解析し、最終的に統合することはわかりました。
じゃあMの具体的な数値はどれぐらいが適切なの？と疑問に思うかなと思います。
この疑問に対しても、高橋先生・伊藤先生のこちらの論文がわかりやすいです。
- 概ね 5～10 では少なすぎ、20～50 程度が適切だと考えられる。
- 欠測率に応じて「20%未満ならば M =20」「20%～30%ならば M = 30」「30%～40%ならば M = 40」「40%～50%ならば M = 50」といった具合に設定することが適切。
- 欠測率に関わらず、M = 100 を超えて得られるものは非常に少ない。
- たとえ M 数を数百まで拡大したとしても、補定値の精度を保証できなくなるおそれがある。
実際の論文ではどう設定しているのかをみると、例えば以下の論文ではM=20に設定されていることがわかります。
（参考：Multicenter Trial of a Combination Probiotic for Children with Gastroenteritis (Stephen B. Freedman et al., November 22, 2018, N Engl J Med 2018;379:2015-26.)）
そのため、総合的に考えると、常にM=50程度に設定しておけば問題なさそうかなと思います。
EZRで多重代入法はできる？
多重代入法の原理はわかったので、実際に多重代入法をやりたい！
無料の統計ソフトであるEZRでは実施できないだろうか？と思うかもしれません。
結露から言えば、EZRのメインメニューでは多重代入法を実施できないです。
しかし、バックグラウンドで動いているRでは問題なく多重代入法を使うことができます。
実際にはmiceというパッケージを使い、手順は以下の3つです。
- miceを使ってM個の補完データを作成する
- withでM個の解析を実施する
- poolで最終的に統合する
Rで多重代入法を実施するプログラム例
では具体的なプログラム例を見ていきましょう。
M=50、Cox回帰を実施する、欠測のあるデータは「dat」という名前でインポートされている前提で例を紹介します。
- miceを使ってM個の補完データを作成する：
tempdat <- mice (dat, m=50, method=”pmm”, pritFlag = FALSE, seed = 123) - withでM個の解析を実施する：
fit <- with(data=tempdat, coxph(formula = Surv(PFS, PFS.status == 1) ~ Grade + Sex, method = “breslow”)) - poolで最終的に統合する：
summary(pool(fit), exponentiate=TRUE, conf.int=0.95)
上記の3つのプログラムを参考にしていただければ、多重代入法を実施できます！
まとめ
いかがでしたか？
この記事では「多重代入法（多重補完法）をわかりやすく解説！EZRでは実施できる？」ということでお伝えしました。
多重代入法（Multiple Imputation）は、医療系の論文でよく使われる方法。
- 多重代入法とは欠測値（欠損値）に対応する方法である
- 多重代入法の概念をわかりやすく解説
- EZRで多重代入法はできる？
ということが理解できたのなら幸いです！！
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
