今日の記事では、SPSSで多変量解析を実施する具体的な手順をお伝えします。
実際のデータを解析する際には、T検定やカイ二乗検定などの単純な検定だけでなく、共変量を調整するような多変量解析を多く実施することがありますよね。
そのため、今回の記事がそのままあなたの実務に役立つと思います。
この記事では、SPSSを用いて多変量解析(重回帰分析)の一つである、共分散分析を実施します。
では、いってみましょう!
SPSSでどんな多変量解析をすればいいかってどう判断するの?

まず重要なのが、あなたの手元にあるデータに対してSPSSのどの多変量解析を実施するのか!?という判断。
これを知らなければ、実務でデータを解析することができませんよね。
どの多変量解析を実施するのか、という判断は、実は簡単です。
目的変数がどんな種類のデータなのか、ということを考えればいいだけ。
- 目的変数が連続量:共分散分析(重回帰分析)
- 目的変数が2値データ(カテゴリカルデータ):ロジスティック回帰
- 目的変数が生存時間データ:Cox比例ハザードモデル
ここで共分散分析(重回帰分析)としているのは、実際には共分散分析と重回帰分析のやり方は一緒だからです。
共分散分析も重回帰分析も、目的変数が連続量であることは同じ。
説明変数にカテゴリカルデータがあるかどうかで呼び方を得ているだけです。
ということなので、この記事では共分散分析(重回帰分析)として区別せずに説明していきます。
そのため、共分散分析(重回帰分析)を実施するには目的変数が連続量であることが必要だと理解できました。
では早速、SPSSで共分散分析(重回帰分析)を実践していきましょう!
SPSSで共分散分析(重回帰分析)を実施する!

SPSSで共分散分析(重回帰分析)を実施します。
共分散分析とは、共変量の影響を除いて群間比較できる、解析手法でした。
そして今回は自治医科大学さんが提供しているサンプルデータの中から「Hb」を使ってみます。
「Hospital」「Sex」「Hb」の3種類のデータがあります。
そのため、性別が共変量だったと仮定して、“性別という共変量の影響を取り除いた病院AとBのHbの値の違いを比較する”ということをやります。
では実際にやっていきましょう!
SPSSに共分散分析(重回帰分析)を実施するためのデータを取り込む
ではここから、SPSSにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
SPSSを開き「ファイル」→「データのインポート」→「CSVデータ」を選択します。
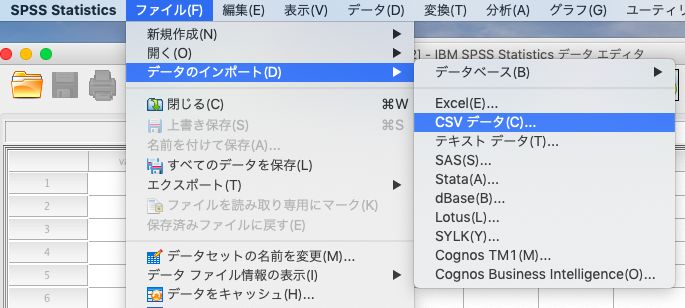
そうすると、以下のような画面になりますので、特にいじらずにOKで大丈夫です。
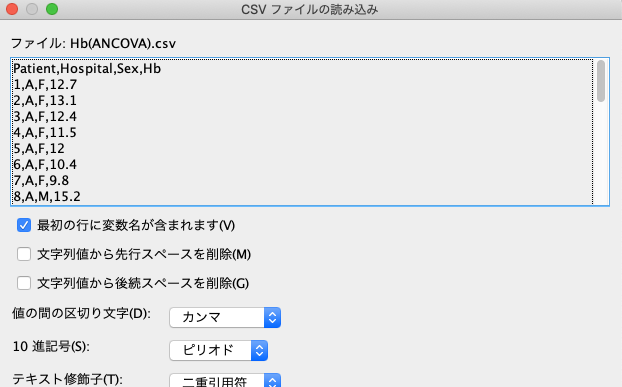
そうすると、以下のようにちゃんとインポートされました。
データの見た目は、エクセルと同じ感じですね。
連続量のデータであれば右揃えでデータが表示され、カテゴリカルデータであれば左揃えでデータが表示されます。

SPSSで共分散分析を実践する!
解析するための準備が整いましたので、早速SPSSで共分散分析を実施してみましょう。
共分散分析を実施するには、下図のように、[分析(A)]→[一般線形モデル(G)]→[1変量]の順にクリックします。
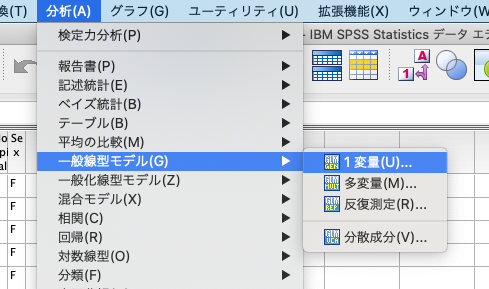
すると以下のボックスが出てきますので、従属変数にHbを入れ、固定因子にHospitalとSexを入れます。
ここで注意したいのは、カテゴリカル変数で調整したい場合には「固定因子」に変数を入れ、連続変数で調整したい場合には「共変量」に変数を入れるということ。
今回は「性別」で調整したいため、「固定因子」に入れます。
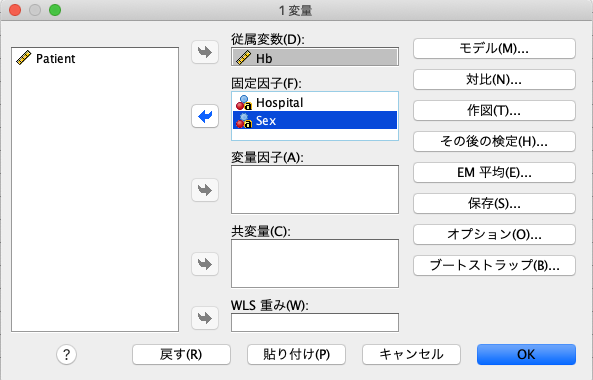
そして、「モデル」をクリックして「項の構築」をクリックします。
固定因子として含めた「Hospital」と「Sex」を主効果としてモデルに含めます。
こうすることで、Hb = a1*Hospital + a2*Sex +b + 誤差というモデルを推定してくれることになります。
この操作をしないと、交互作用項までデフォルトで入ってしまいます。
つまり、Hb = a1*Hospital + a2*Sex a3*Hospital*Sex +b + 誤差を推定してしまう、ということです。
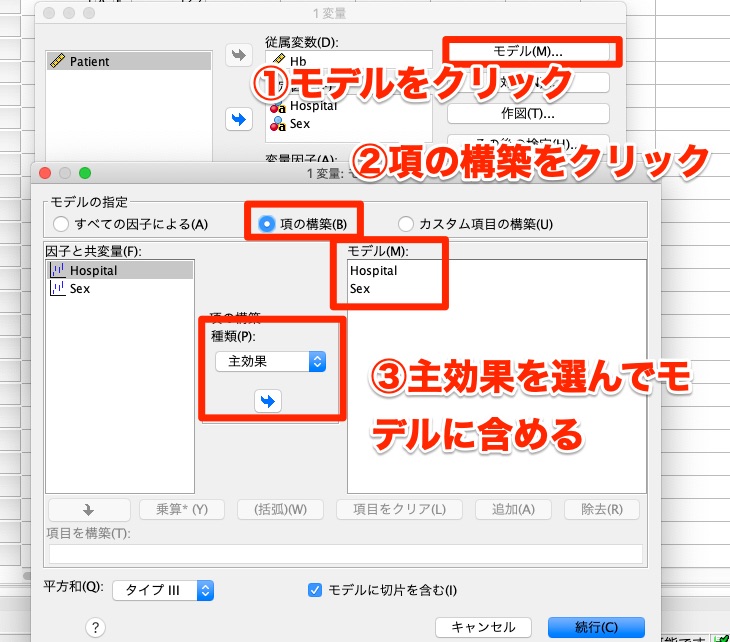
また、オプションをクリックして「記述統計」と「パラメータ推定値」にチェックを入れておきます。
そうすることで、P値だけじゃなく、情報量をリッチにできます。
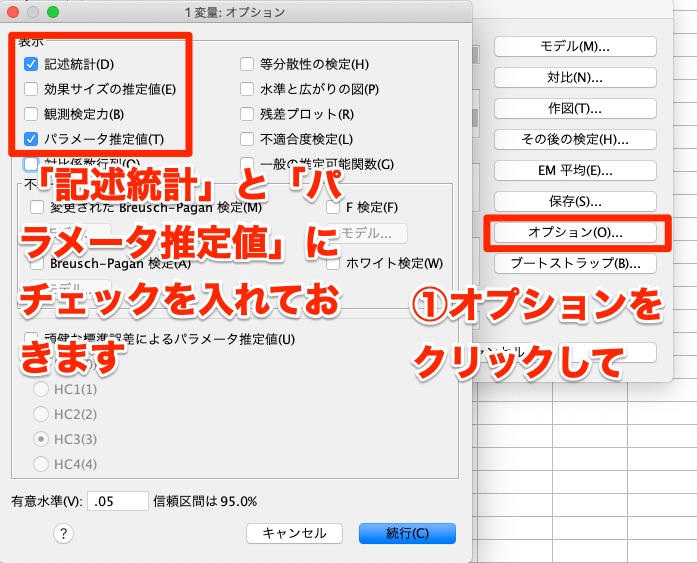
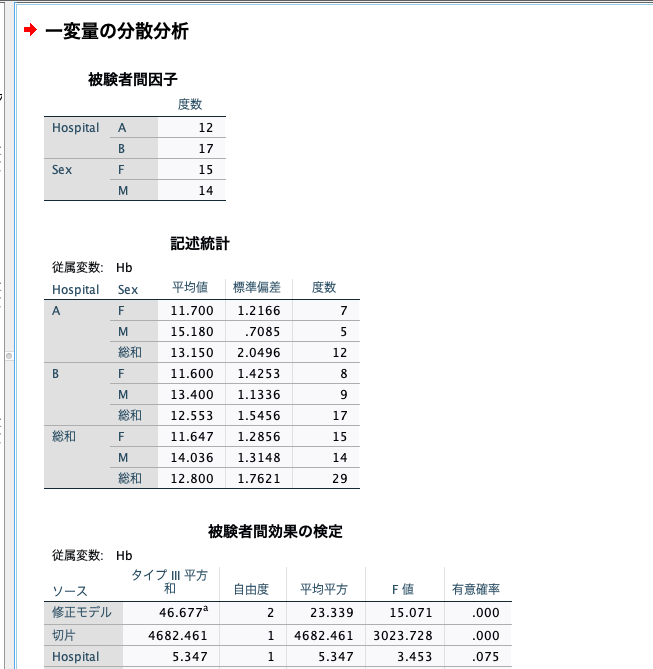
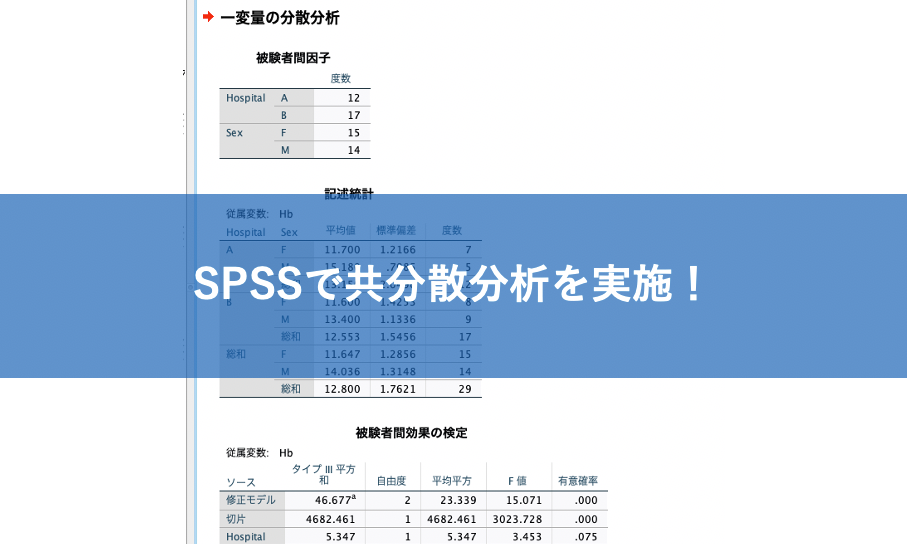
すると、下記のように共分散分析を実施した結果が出てきました。
SPSSで実施した共分散分析(重回帰分析)の結果を解釈しよう
実際にSPSSで共分散分析が実施できました。
では、結果の解釈をしていきましょう。
共分散分析の結果の前に要約統計量
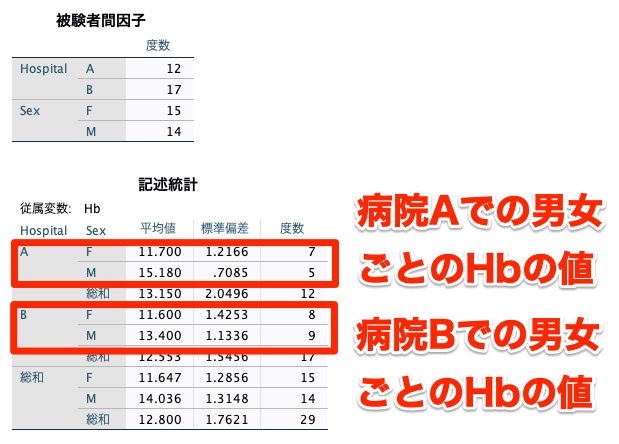
まずは、要約統計量をみてみます。
SPSSのオプションで要約統計量を出力してくれるようにチェックを入れたので出力されていますね。
- HospitalAとBのそれぞれの度数
- 男女のそれぞれの度数
- 病院Aでの男女ごとのHbの要約統計
- 病院Bでの男女ごとのHbの要約統計
なんかが出力されており、これを見るだけでもかなりの情報を読み取れます。
少なくとも、男女ではHbの値が違いそうだな、ということまでは読み取れますね。
共分散分析表とパラメータ推定値の結果解釈
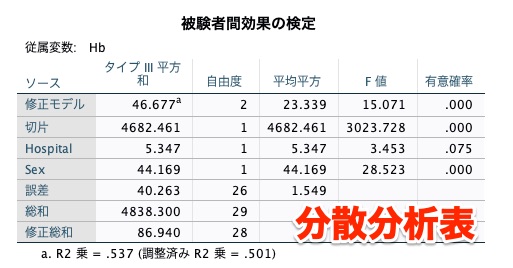
まずは共分散分析を実施した結果の表の解析結果です。
かなりの情報量が詰まっていますね。
下記の表の見方は、分散分析表と同じです。
なので、分散分析表の解説をしている記事を基にして、F値やP値の意味なんかを理解しておきましょう。
自由度についてはおさらいしておくといいですね。
統計検定2級でも、回帰分析の結果から自由度を読み取らせる問題が頻出するので、ぜひとも見方を覚えましょう。
今回は、説明変数(HospitalとSex)で自由度が2、誤差(Residual)で26、切片で1と読み取れます。
ここからも、データ数は2+26+1=29(総和)であることが分かりますね。
そして、もっとも得たかった結果が、以下のパラメータ推定値ですね。
ここには、説明変数で入れた「Hospital」と「Sex」の偏回帰係数(一般的には回帰係数)の結果が記載されています。
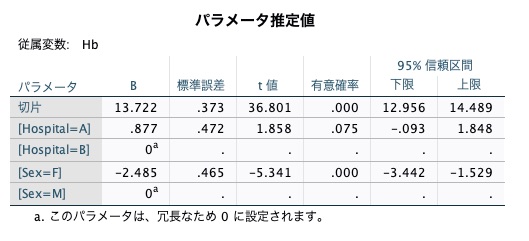
Bの列は、回帰係数の点推定値です。
有意確率は、“回帰係数が0である”という帰無仮説に対する検定結果です。
つまりここのP値が0.05を下回った場合に、回帰係数は0ではなさそうだ、ということが言えます。
更に言い換えると、P値が0.05を下回った場合には“この説明変数は目的変数に対して影響を与えていそうだ”ということが言えます。
今回の結果でいうと、HospitalはP=0.075なので有意水準5%で有意差なし。
性別は有意差あり、です。
95%信頼区間も出力されています。
ここでの95%信頼区間は、一般的な95%信頼区間と、解釈の仕方は一緒です。
今回知りたかったことは、性別が共変量だったと仮定して、“性別という共変量の影響を取り除いた病院AとBのHbの値の違いを比較する”ということです。
今回の結果から、Hbの値に関して性別の影響を除いて病院AとBを比較したら、有意差はなかった、という結論を導くことができます。
共分散分析(重回帰分析)じゃなく、共変量で調整しない解析をするとどう違いが出てくるの?

共分散分析は、共変量の影響を除いて群間比較できる、解析手法でした。
今回のデータでは、Sexを共変量(交絡バイアスを引き起こす交絡因子)としていましたよね。
では、共変量がなかった時に本当に結果が変わるのか!?ということをやってみましょう。
やり方の手順は先ほどと同じで、説明変数にはHospitalの1つだけ入れます。
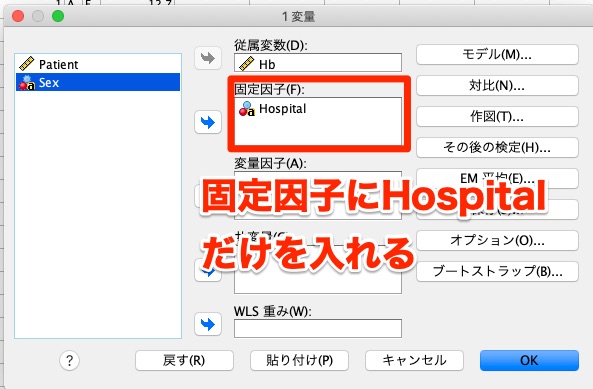
「モデル」や「オプション」も先ほどと同じ設定にしてくださいね。
すると、下記のような結果が出力されています。(パラメータ推定値だけ載せておきます)
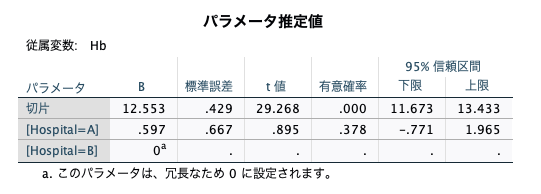
Sexで調整した場合にはP=0.075でしたが、Sexで調整しないとP=0.378という結果が出ました。
Sexによる調整の有無が、Hospitalの結果に影響を少なからず与えていたことが分かります。
SPSSで共分散分析まとめ
今回は、SPSSで多変量解析の一つである共分散分析を実施しました。
これを実践し、結果の解釈をすることができれば、必ず実務で役に立ちます。











コメント