この記事では、SPSSでマンホイットニーのU検定を実施する方法をお伝えします。
マンホイットニーのU検定は、ウィルコクソンの順位和検定と同じ検定です。
なので、ウィルコクソンの順位和検定で覚えている方も多いかも知れませんね。
マンホイットニーのU検定とは、連続変数に対するノンパラメトリックな検定手法。
一方のパラメトリックな検定は、T検定でしたね。
ということで、今回の記事はマンホイットニーのU検定をSPSSで実施する方法に加えて、同じデータに対してT検定を実施した時の違いまで解説します。
SPSSでマンホイットニーのU検定を実施するために必要なデータを読み込む

まずは、マンホイットニーのU検定を実施するために必要なデータを解説します。
マンホイットニーのU検定は、2群の連続量を対象としたノンパラメトリック検定でした。
ということは、用意するデータは以下の2つを満たす必要があります。
- 連続量のデータが必要。
- 2群の群間比較をするので、2つのカテゴリを持つ、カテゴリカルデータが必要。
SPSSでマンホイットニーのU検定を実施するのに使用するデータ
ということで、SPSSでマンホイットニーのU検定を実施するデータです。
今回はA群、B群の2つの群で、LDHの平均値を比較してみます。
(データは架空のデータです。)
実際には、SPSSでT検定を実施したときと同じデータを使います。
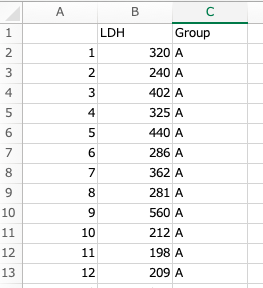
LDHが連続データで、Groupが群を示した変数です。
A群13例、B群11で、計24症例分のデータがあります。
SPSSにマンホイットニーのU検定を実施する基となるデータを読み込む
ではここから、SPSSにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
SPSSを開き「ファイル」→「データのインポート」→「CSVデータ」を選択します。
そうすると、以下のような画面になりますので、特にいじらずにOKで大丈夫です。
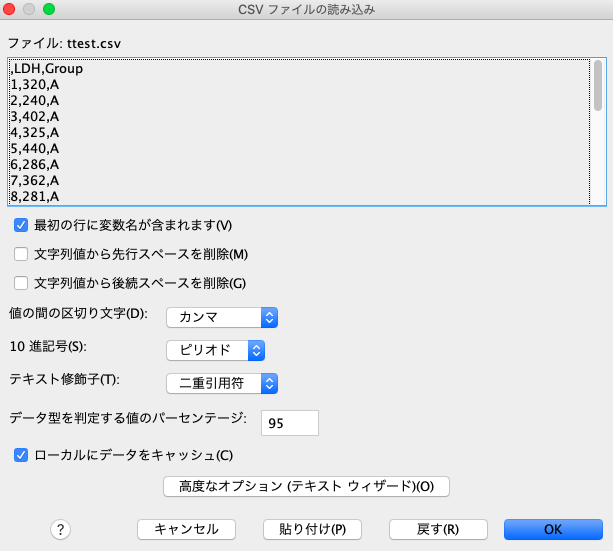
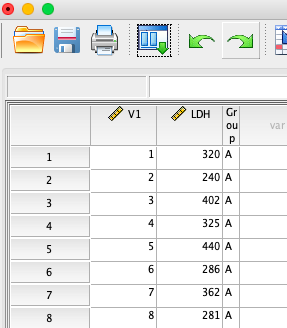
そうすると、以下のようにちゃんとインポートされました。
データの見た目は、エクセルと同じ感じですね。
連続量のデータであれば右揃えでデータが表示され、カテゴリカルデータであれば左揃えでデータが表示されます。
SPSSでマンホイットニーのU検定を実践する!
解析するための準備が整いましたので、早速SPSSでマンホイットニーのU検定を実施してみましょう。
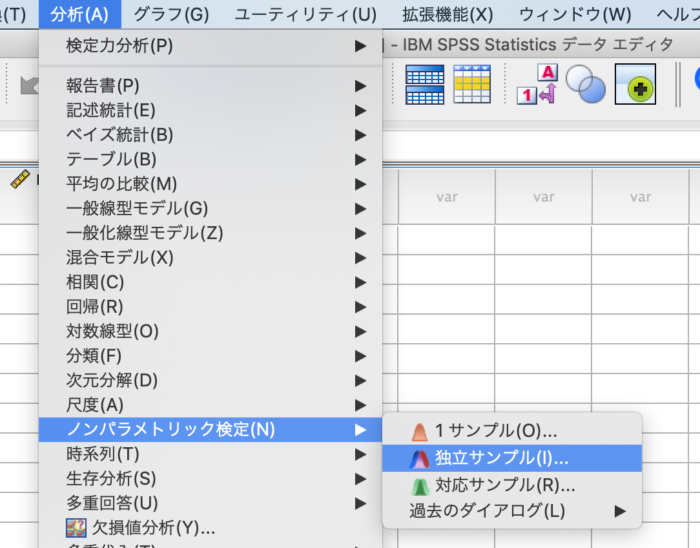
マンホイットニーのU検定を実施するには、下図のように、[分析(A)]→[ノンバラメトリック検定(N)]→[独立サンプル]の順にクリックします
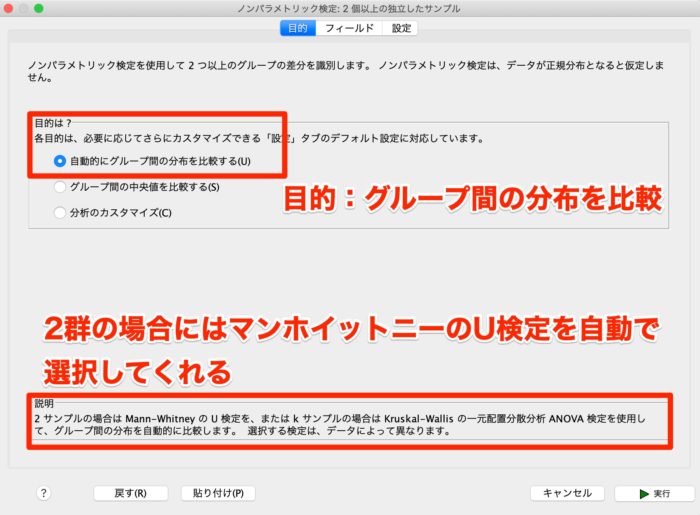
すると以下のボックスが出てきますので、「目的」は「自動的にグループ間の分布を比較する」にチェックを入れます。
すると、2群の場合には自動的にマンホイットニーのU検定を実施してくれます。
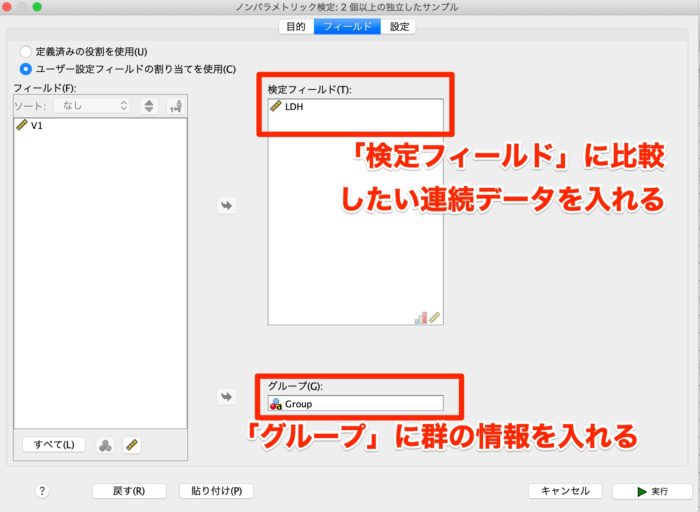
「フィールド」で実際に解析したい列を選択します。
「検定フィールド」には連続変数であるLDHを、「グループ」は比較したい群情報であるGroupを選択します。
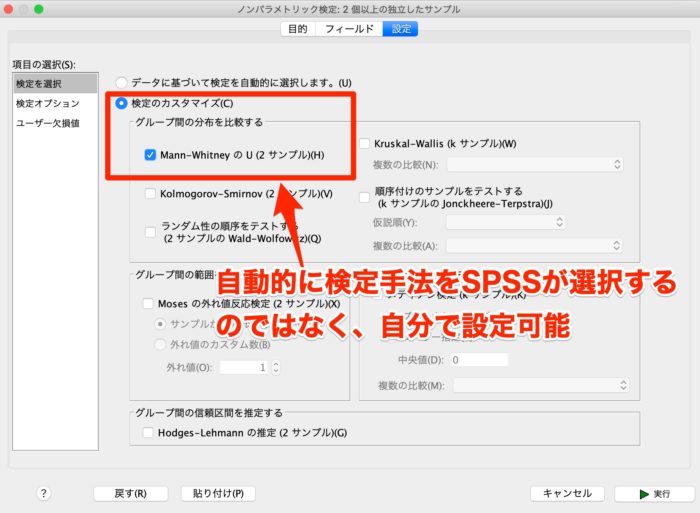
このまま実行してもいいのですが、「設定」で検定をカスタマイズすることもできます。
自動的にSPSSに検定を選んでもらってもいいですが、自分で選択するのもOKです。
今回の記事では、検定のカスタマイズでマンホイットニーのU検定を選択して実行します。
すると、下記のようにマンホイットニーのU検定が実施した結果が出てきました。

SPSSでは以下のような結果を出力してくれます。
- マンホイットニーのU検定の結果の結論
- マンホイットニーのU検定の要約統計量
- 各グラフ
SPSSでマンホイットニーのU検定を実施した結果の解釈
実際にSPSSでマンホイットニーのU検定が実施できました。
では、結果の解釈をしていきましょう。
SPSSで実施したマンホイットニーのU検定のログを確認する
まずは、マンホイットニーのU検定のログを確認します。
ログ自体は確認しなくても良いことが多いですが、例えば論文を出したいために、ちゃんとQCをしたい場合などは確認する必要がありますね。
独立した二人で同じデータで解析を実施し、ログがちゃんと同じになるかどうかを確認することが大事だったりします。
解析結果が合わない時も、ログを確認することで、どこが違っているかを確認することができます。
そのため、解析結果のログを確認する習慣をつけましょう。
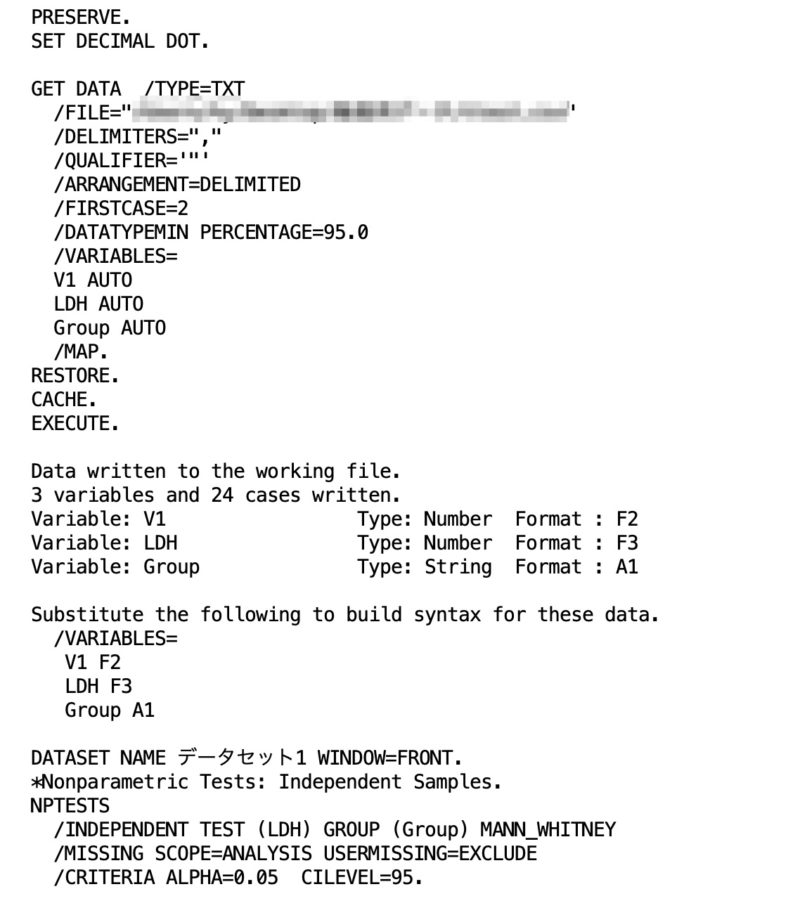
今回の記事では、詳細はスキップします。
SPSSでマンホイットニーのU検定を実施した結果の解釈:検定の結論が出力される
まずはマンホイットニーのU検定を実施した結論が出力されています。
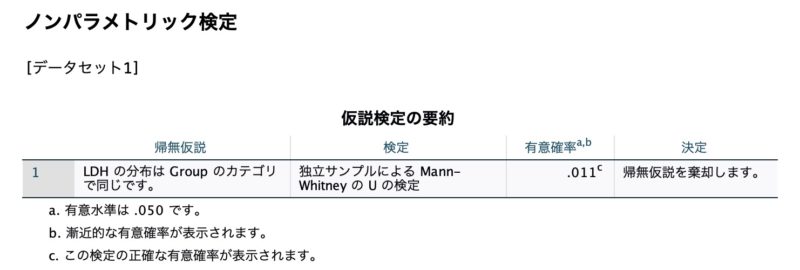
ちゃんと帰無仮説が記載されているのが素晴らしいですね。
そのため、今回の結果ではP=0.011ということで、有意水準の0.05を下回っているから有意(帰無仮説を棄却)という結論になります。
SPSSでマンホイットニーのU検定を実施した結果の解釈:各群のヒストグラムが作成される
そして、各群のヒストグラムも出力されています。
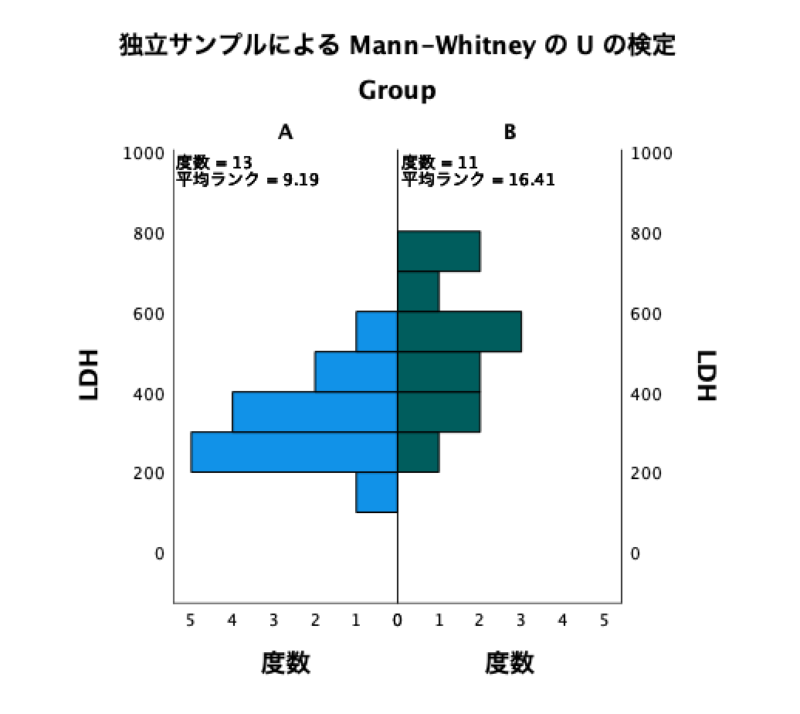
SPSSでヒストグラムを作ることもできますが、一つの解析でちゃんとグラフも出力されるのはいいですよね。
同じデータでマンホイットニーのU検定とT検定の違いは?
以上の手順で、マンホイットニーのU検定をSPSSで実施することができました。
次なる疑問は、同じデータでT検定を実施すると結果はどうなるのか!?ということ。
今回はT検定を実施した際と同じデータを使用しましたので、P値を比較しましょう。
同じデータでT検定を実施すると、P=0.005(等分散の場合)が得られていますね。
つまり、T検定の結果の方が、P値が小さいことが分かります。
T検定とU検定の検定結果の違いはこのような関係になります。
| データの分布 | T検定(パラメトリック) | ウィルコクソンの順位和検定(ノンパラメトリック) |
| 正規分布 | ◎ | ◯ |
| 正規分布ではない | × | ◯ |
今回のデータは正規分布に近かったという考察ができます。
本当に正規分布なのか!?ということを確認するために、ヒストグラムを再度確認してみましょう。

どちらの群も真ん中が1番度数が多く、正規分布からそれほど大きく離れていないことがわかります。
SPSSでマンホイットニーのU検定まとめ
今回は、SPSSでマンホイットニーのU検定を実施しました。
ノンパラメトリックな検定であるマンホイットニーのU検定はいろんなところで使えますので、やり方や結果の解釈を確実にできるようになりましょう。










コメント
コメント一覧 (1件)
[…] >>SPSSでマンホイットニーのU検定を実施 […]