この記事では、幾何分布について詳しくお伝えします。
- 幾何分布ってどんな分布?
- 幾何分布の平均値や分散はどうなっているの?
といった疑問についてお答えしていきます!
正規分布よりは重要性が落ちる幾何分布ですが、この知識を知っておくことで医療統計の様々なところで応用できるため、ぜひ理解していきましょう!
幾何分布とは?例題を用いてわかりやすく解説!

例えば、サイコロを1の目が出るまでひたすら振り続けるときに、1の目が出るまでに無駄にサイコロを振り続ける回数の分布が幾何分布(geometric distribution)の具体例となります。
5回目にサイコロの1の目が出るとすると、その確率は、(1-1/6)×(1-1/6)×(1-1/6)×(1-1/6)×1/6=0.0803755・・・となる。
もう少し厳密にいうと、成功確率pの独立なベルヌーイ試行において、最初の成功が起こるまでの失敗の回数Xが従う確率分布のことを幾何分布といいます。
ここで少し注意して欲しいことは、「連続して失敗する回数」ではなく「成功するまでにかかる回数」が従う分布を幾何分布と言う場合もあるということ。
その場合回数のカウントが1ずれるので注意して下さい。
幾何分布とは成功確率pの独立なベルヌーイ試行において、最初の成功が起こるまでの失敗の回数nが従う確率分布
成功確率pの独立なベルヌーイ試行において、最初の成功が起こるまでの失敗の回数nが従う確率分布のことでしたよね。
幾何分布の確率関数は次のようになります。

この式のように等比数列(幾何数列)になっているので幾何分布という名前がついている。
最初に紹介したサイコロを1の目が出るまでひたすら振り続けるときに、1の目が出るまでに無駄にサイコロを振り続ける回数の幾何分布についてグラフを書くと以下のようになります。
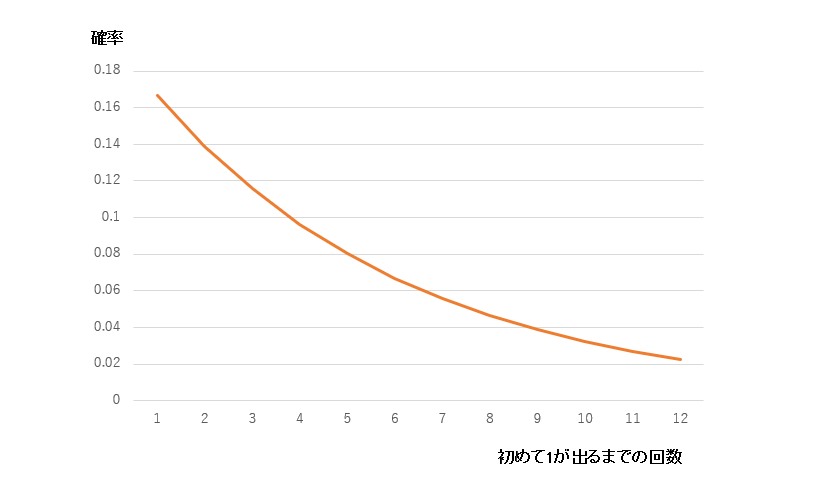
幾何分布の具体例を3つ紹介します。
幾何分布の例題1
都市活動の持続および消滅過程をモデル化することを考えます。
簡単のため、都市活動の消滅(廃業、移転、建物の建て替えによる一時移転などを含む。)が時刻および発生からの経過時間にかかわらず一定の比率で起こると仮定する。
さらに、時刻は年を単位とする離散値を取ると仮定する。都市活動が 1 年間に消滅する確率を p とすると、余命が t 年である確率は幾何分布に従う。
確率関数は以下のようになります。
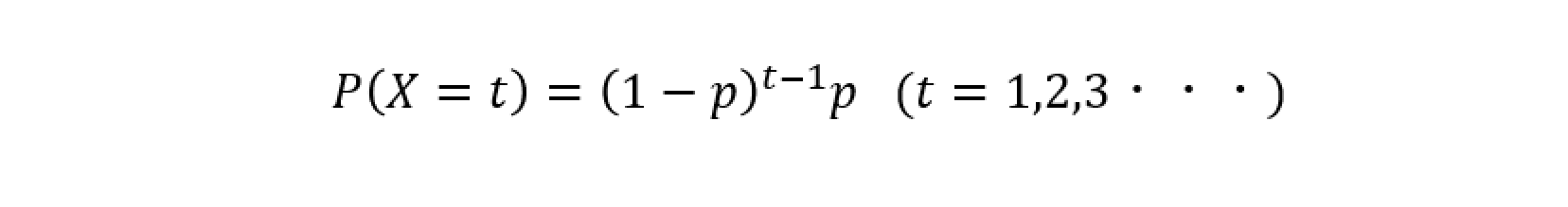
幾何分布の例題2
ある半導体デバイスの母集団から抜き取った 1 個のサンプルについてテストを行う。
テスト結果は、「故障している、不良」と「異常なし、合格」の二つの場合のいずれかだけで、判定保留や特別採用などの例外はないとする。
この「サンプリング→テスト→判定」のサイクルを n 回繰り返し試行します。1 回のテストで「故障している、不良」の起こる確率を p、「異常なし、合格」の起こる確率を 1-p とし、各回のテストにわたって pと1-p の値は一定とします。
また、各回のテスト結果は独立であって他の回のテスト結果に影響を与えないものとする。
すなわち、ベルヌイ試行になっているとすわけです。
第 n 回目のテストで初めて「故障している、不良」である半導体デバイスが発見されるという事象の起こる確率は幾何分布に従う。
確率関数は以下のようになります。

幾何分布の例題3
あるウイルスが薬剤耐性変異を獲得する確率をpとするとき、このウイルスが薬剤耐性変異を獲得するまでの継代回数nは幾何分布に従う。
確率関数は例2と同様です。
幾何分布においてその試行回数nは、初めてその事象が起こるまでの待ち時間とみなすことができ、そのため幾何分布は離散的な待ち時間分布ともよばれます。
また、幾何分布は、無記憶性を持つ唯一の離散確率分布と言われる。
これがどういうことか理解するために、サイコロを例に考えましょう。
サイコロを振ることを繰り返して少なくとも n 回1の目が出なかったという情報が与えられたときに、1の目が出るまでにサイコロを振る回数が n + k を超える条件付き確率は、情報が与えられない場合の確率(すなわち、今すべてを忘れて改めてサイコロを振る行為を開始して、1の目が出るまでにサイコロを振る回数が k 回を超える確率)に等しいという意味。
例えば、宝くじの購入において負けが続くと、しばしば「運がたまっている」とか「そろそろ勝ちが巡ってくる」といった考えに陥ることがあります。
ところが、試行の独立性を仮定する限りにおいては、この考えは間違いであり、負けが続いているという情報は未来の確率に何の影響も与えないということが、無記憶性からいえる。
この逆、すなわち無記憶性を持つ離散型確率分布が幾何分布のみであることも、比較的容易に示される。
無記憶性の証明は以下のとおり。
ある事象が生じる確率がpのベルヌーイ試行において、n回連続でこの事象が生じず、n+1回目で初めてこの事象が生ずる確率P(X=n)は、
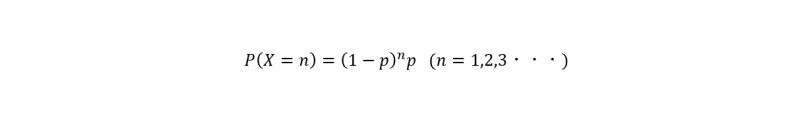
であるので、少なくともn回以上連続でこの事象が起きない確率P(X≧n)は、
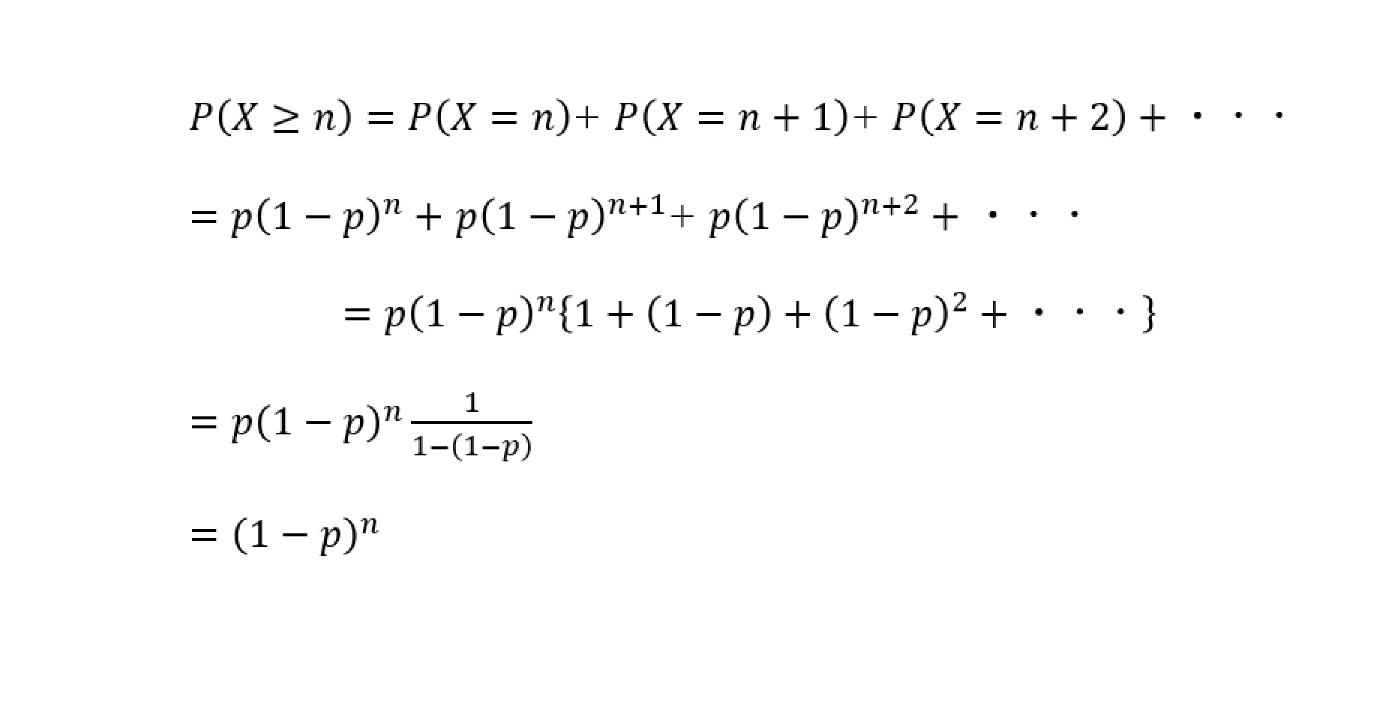
次に、n回連続でこの事象が生じず、n+k回連続でこの事象が生じない確率は、P(X≧n)という前提のもとで、P(X≧n+k)が生じる条件付き確率P(X≧n+k|X≧n)になるので、
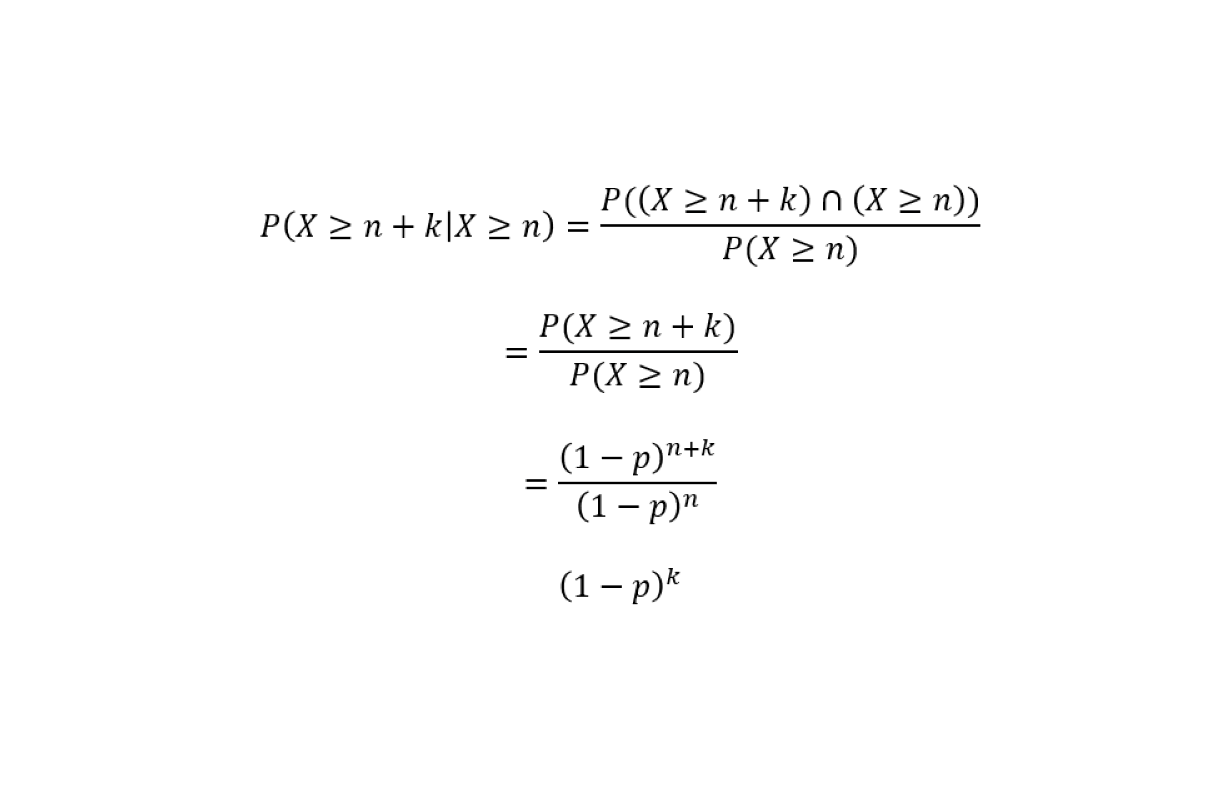
よって、P(X≧n+k|X≧n)=P(X≧k)
これで、無記憶性が示された。
無記憶性を持つ離散型確率分布が幾何分布のみであることの証明は以下のとおり。
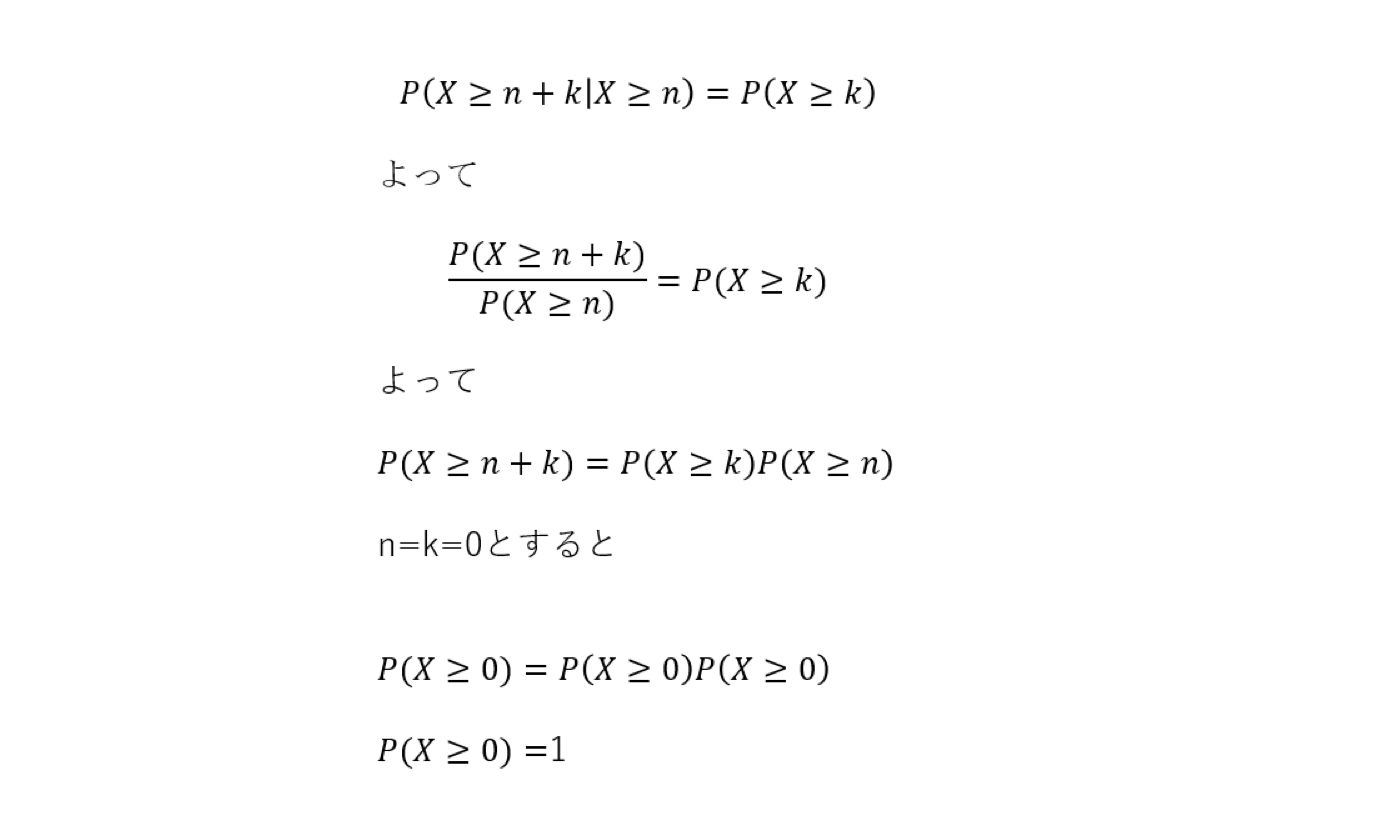
次にk=1とすると、

幾何分布の期待値(平均)と分散はどうなっている?
幾何分布の期待値(平均)は、成功確率をpとすると1/p。ただ、分散は複雑。
幾何分布の期待値(平均)は、初めてその事象が起こるまでの待ち時間となるため、成功確率をpとすると、1/pとなります。
分散は直感的には求まりません。
幾何分布の期待値(平均)と分散の求め方・証明は?
幾何分布の期待値(平均)と分散の証明は意外と簡単
幾何分布の期待値(平均)は以下のように求まります。


幾何分布の分散は以下のとおり。


幾何分布まとめ
幾何分布とは何かについてお分かりいただけたでしょうか。
サイコロを1の目が出るまでひたすら振り続けるときに、1の目が出るまでに無駄にサイコロを振り続ける回数の分布という具体例を考えれば、理解しやすいと思います。
また、離散型確率分布においては、無記憶性を持つものが幾何分布のみであるこも大切。
くれぐれも例えば、ギャンブルにおいて負けが続いているからといって、「運がたまっている」とか「そろそろ勝ちが巡ってくる」といった考えに陥って、ギャンブルを続け挙句の果てに破産するということがないように。
>>一様分布とは?
>>正規分布とは?












コメント