この記事では、指数分布について詳しくお伝えします。
- 指数分布ってどんな分布？
- 指数分布の平均値や分散はどうなっているの？
といった疑問についてお答えしていきます！
正規分布よりは重要性が落ちる指数分布ですが、この知識を知っておくことで医療統計の様々なところで応用できるため、ぜひ理解していきましょう！
Contents
指数分布とは？例題で理解しよう！
指数分布（exponential distribution）とは、ざっくり言うとランダムなイベント（事象）の発生間隔を表す分布です。
少し小難しい表現で定義すると、指数分布とは、イベントが連続して独立に一定の発生確率で起こる確率過程（時間とともに変化する確率変数のこと）に従うイベントの時間間隔を記述する分布です。
言い換えると、指数分布とは、全く偶然に支配されるイベントがその根底にあるとして、そのイベントが起こらない時間間隔0～xが存在し、次のある短い時間dxの間にそのイベントが起こる様な確率の分布とも言える。
確率分布関数や確率密度関数がシンプルで覚えやすいのもいい。
現実の社会や自然界には、指数分布に従うと考えられイベントがたくさんあり、その例は
- 交通事故の発生
- 放射性物質の崩壊
- 銀行窓口への来客
- 人の死亡
- 機械の故障
などさまざま。
従って、指数分布をマスターすれば世の中の多くの問題が解けるということです。
指数分布とは、イベントが独立に、起こる頻度が時間の長さに比例して、単位時間あたり平均λ回起こる場合の確率分布
指数分布の条件：ポアソン分布との関係とは？
それでは、指数分布についてもう少し具体的に考えてみましょう。
指数分布とは、以下の①と②が同時に満たされるときにそのイベントが起きる時間間隔xの分布のこと。
- あるイベントは独立に、起こる頻度が時間の長さに比例して、単位時間あたり平均λ回起こる。
- そのイベントの起こる回数はポアソン分布に従う。
では、指数分布の分布関数をF(x)として、この関数の具体的な形を計算してみましょう。
あるイベントが起こらない時間間隔0～ xが存在し、次のある短い時間dxの間にそのイベントが起こるので、F(x+dt)－F(x)・・・① は、ある短い時間dxの間にあるイベントが起こる確率を表す。
一方、時刻0から時刻xまではあるイベントは発生しないので、その確率は１－F(x)。
あるイベントは、単位時間あたり平均λ回起こるので、時刻0から時刻xまではあるイベントは発生せず、その次の瞬間の短い時間dxの間にそのイベント起こる確率は(１－F(x))×dx×λ・・・②
①＝②なので、F(x+dx)－F(x)＝(１－F(x))×dx×λ
式変形すると、(F(x+dx)－F(x))／dx＝(１－F(x))×λ となります。
左辺はF(x)の微分になるので、さらに式変形すると
F'(x)／(１－F(x))＝λ となり、
この式の両辺をxで積分して、F(0)＝0を使い、F(x)について解くと、
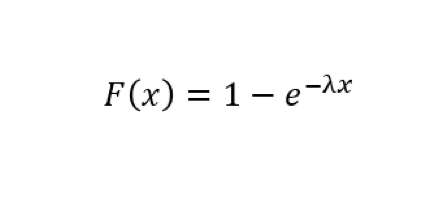
が得られます。
確率密度関数は、分布関数を微分したものですから、
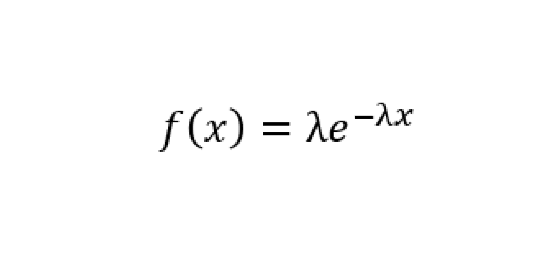
となる。
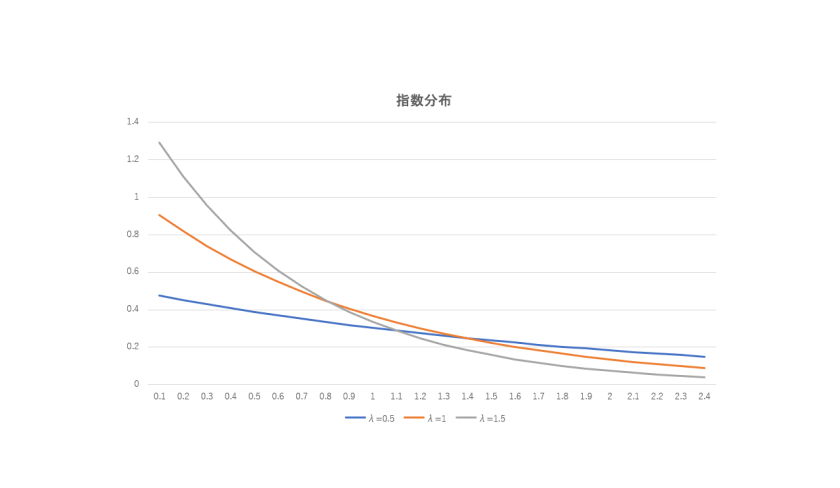
この指数分布のグラフをλ=0.5、1.0、1.5の場合に描くと以下のような感じ。
指数分布を例題を用いてさらに理解する！
指数分布の形が分かったところで、次のような問題を考えてみましょう。
例題
1時間に平均20人が来る銀行の窓口がある場合に、この窓口にある客が来てから次の客が来るまでの時間が3分以内である確率はどうなるか。
まずは時間の単位をそろえます。
3分=1／20時間なので、次の客が来るまでの時間が1／20時間以下となる確率を求める。
問題文からλ=20。
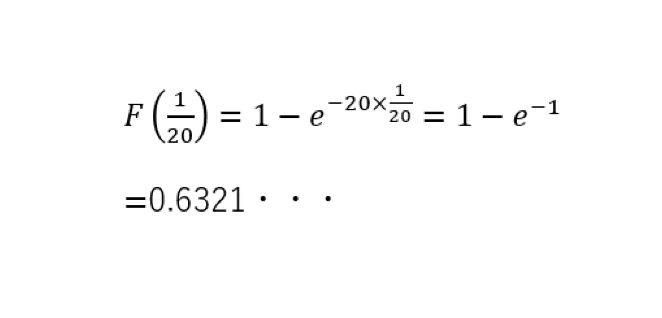
この窓口にある客が来てから次の客が来るまでの時間が3分以内である確率は、約63%であるということです。
このように指数分布は、銀行窓口の待ち時間などの身近な問題から放射性同位体の半減期の問題などの科学的な問題、あるいは電子部品の予測寿命の計算などの生産活動に関する問題など、さまざまな問題に応用が可能で重要な確率分布の一つであると言える。
指数分布の期待値（平均）と分散はどうなっている？
指数分布の期待値（平均）は指数分布の定義から明らか
まず、期待値(expctation)というものについて理解しましょう。
指数分布のような確率密度関数が連続関数であるような確率分布の期待値は、確率変数と確率密度関数の積を定義域に亘って積分したもののことです。
確率変数の分布を端的に示す指標といえる。
指数分布の期待値は直感的に求めることができる
ところが指数分布の期待値は、上のような積分計算を行わなくても、実は定義から直感的に求めることができます。
どういうことかと言うと、指数分布とはランダムなイベント（事象）の発生間隔を表す分布で、一方、イベントは単位時間あたり平均λ回起こるという定義だったので、イベントの平均的な発生間隔は、1／λ。
すなわちこれが期待値ということ。
指数分布の分散
次に、分散について理解しましょう。
期待値だけでは、ある確率分布がどのくらいの広がりをもって分布しているのかがわからない。
そこで、平均の周りにどの程度分布するかの指標として分散 (variance) がある。
平均と合わせると、確率分布を測定するときの良い指標となる。
確率密度関数が連続関数であるような確率分布の分散は、確率変数と平均との差の2乗と確率密度関数の積を定義域に亘って積分したもののことです。
ただ、上の定義式のまま分散を計算しようとすると、かなりの計算量となる場合が多いので、分散の定義式を変形して、以下のような式にしてから分散を求める方が多少計算が楽になる。
分散＝確率変数の2乗の平均－確率変数の平均の2乗
指数分布の分散は直感的には求まりませんが、上の定義に従って計算すると指数分布の分散は期待値の2乗になります。
すなわち、指数分布の場合、イベントの平均的な発生間隔1／λの2乗だけ、平均からぶれるということ。
指数分布の期待値（平均）と分散の求め方・証明は？
指数分布の期待値（平均）と分散の求め方は結構簡単
指数分布の期待値（平均）は、「確率変数と確率密度関数の積を定義域に亘って積分する」という定義式に沿ってとにかくひたすら計算すると求まります。
では実際に計算してみましょう。
上のような式変形だけで結構あっさり計算できる。
次に、指数分布の分散は、確率変数と平均との差の2乗と確率密度関数の積を定義域に亘って積分したものですが、「指数分布の期待値（平均）と分散はどうなっている？」で説明した必殺技
分散＝確率変数の2乗の平均－確率変数の平均の2乗
を使って求めることにします。
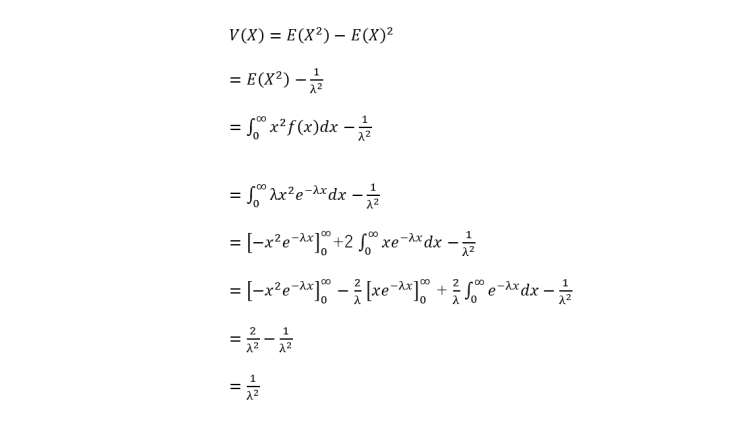
というようにこれもそこそこの計算量で求めることができる。
指数分布の平均も分散も高校数学レベルの部分積分をひたすら繰り返すことで求めることが出来ることがお分かりいただけたでしょうか。
こんな計算忘れちゃったよという方は、是非最低でも1回は紙と鉛筆（ボールペン？）を持ってきて実際に計算するといいと思いますよ。
数式は日本語の文章などとは違って眺めるだけでは身に付かない。
とにかく手を動かすことをオススメします！
指数分布についてまとめ
指数分布は、ランダムなイベントの発生間隔を表すシンプルな割に適用範囲が広い重要な分布
指数分布の概要が理解できましたでしょうか。
また、指数分布に興味を持っていただけたでしょうか。
指数分布は、ランダムなイベントの発生間隔を表す分布で、交通事故の発生に関して損害保険の保険料の計算に使われていたり、機械の故障について産業分野で、人の死亡に関しては生命保険の保険料の計算で使われていたり、放射性物質の半減期の計算については原子核物理学の分野で使われていたりと本当に応用範囲が幅広い。
確率密度関数や確率分布関数の形もシンプルで確率の計算も解析的にすぐ式変形ができて計算し易く、平均や分散も覚えやすく応用範囲も広い確率分布ですので、是非よく理解して自分のものにしてくださいね。
＞＞一様分布とは？
＞＞正規分布とは？
＞＞幾何分布とは？
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
