今回の記事では「四分位範囲(IQR)とは?箱ひげ図との関連や論文の記載方法までわかりやすく解説」ということでお伝えします。
- 四分位範囲とはそもそもどういったことを示しているの?
- 四分位範囲と箱ひげ図との関係は?
- 四分位範囲は何のために使われる?
- 四分位範囲を実際に論文で記載する方法は?
といったことがわかるようになりますよ!
四分位範囲(IQR)とは?箱ひげ図との関連も

まずは四分位範囲について全体像をお伝えします。
四分位範囲を理解するには、まず、四分位数(しぶんいすう)を理解する必要があります。
四分位数とはその文字の通り「得られている全部のデータを全部で4つに分けるための数値」ということ。
具体的には、25%点、50%点、75%点の3つ。
この3つの数値があることで、全部のデータを小さい方から順に並べると「0%点〜25%点」「25%点〜50%点」「50%点〜75%点」「75%点〜100%点」という感じで、4つの領域に分けることができます。
25%点、50%点、75%点の3つ(0%点、100%点も含めると5つ)があることで、得られている全部のデータを4つの領域に分けられましたよね。
四分位数は、データを小さい順に並べて、小さいものから以下の通りに名前が付けられています。
- 25パーセント点=第一四分位数
- 50パーセント点=第二四分位数
- 75パーセント点=第三四分位数
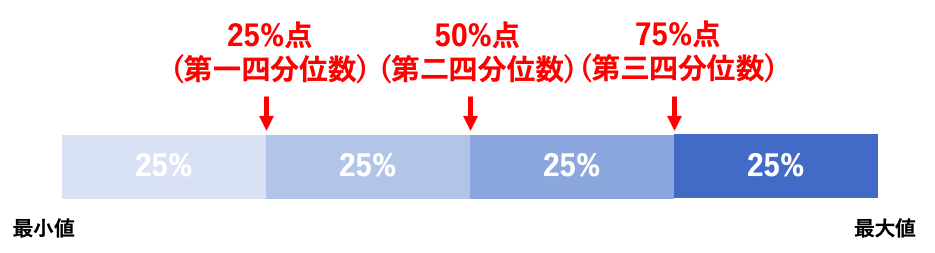
四分位数がわかると四分位範囲の定義は簡単で、四分位範囲とは「25%点から75%点の間」のことを指します。
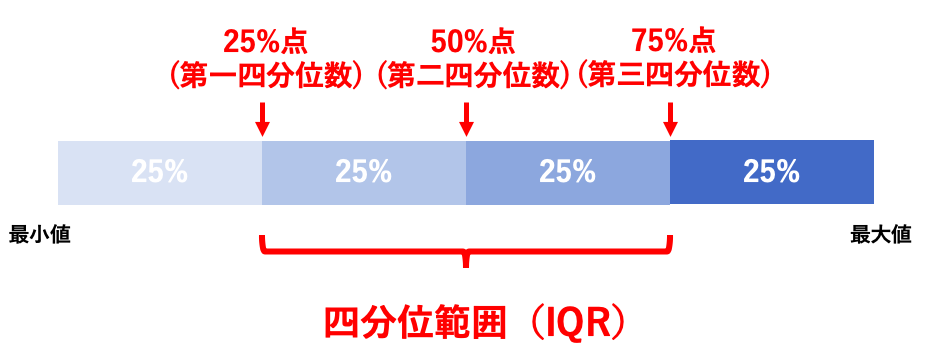
そして0%点は「最小値」という名前がついていて、100%点は「最大値」という名前がついていて、最大値と最小値の間のことを「範囲(英語ではRange)」と呼びます。
50%点は「中央値(メジアン、メディアン)」という名前がついているのです。
箱ひげ図の箱が四分位範囲を示している
というのも、箱ひげ図にある「箱」の部分が、そのまま四分位範囲を示しているからです。
仮に箱ひげ図のひげの部分を最大値と最小値に定義したとすると、箱ひげ図は以下の通りのデータを示していることになります。
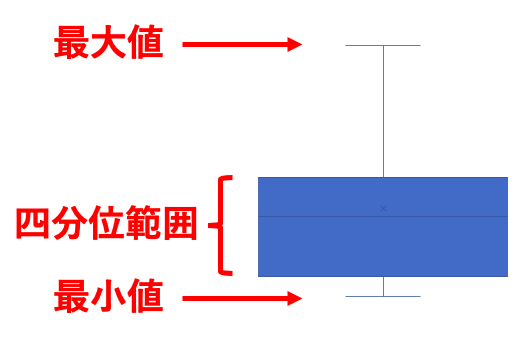
四分位範囲(IQR)とはなぜ何のために使われる?

四分位範囲がどのような定義なのかはわかりました。
じゃあ次に疑問になるのは「四分位範囲は何のために使われているのか」ということ。
結論から言えば、データのばらつきを表すために使われます。
四分位範囲が意味するところは、「得られているデータの真ん中半分はここからここぐらいまで」ということです。
なので、データのばらつきを表しています。
四分位範囲は分散や標準偏差とどう違う?
でもここでさらなる疑問が。
データのばらつきの指標としては、分散や標準偏差もあるけど、分散や標準偏差と四分位範囲はどう違うのか?ということ。
結論から言えば、分散や標準偏差はデータが正規分布に従っている時に最適なデータのばらつき指標ですが、四分位範囲はデータがどんな分布かによらず使うことができる、という点が違います。
多くのデータが正規分布に従っているため、平均値や標準偏差(分散)を目にすることが多いことは確か。
でも、ノンパラメトリック検定であるマンホイットニーのU検定(ウィルコクソンの順位和検定)が適しているようなデータであれば、中央値と四分位範囲を示すことの方が最適なのです。
検定ではノンパラメトリック検定を実施しているのに、要約統計量として平均値と標準偏差(分散)が示してあると、かなりチグハグ感のあるデータ解析になっているな、という印象を持ちます。
また、中央値と標準偏差をセットで使っている場面も散見されます。
- 中央値を用いるなら、ばらつきの指標は四分位範囲を使う
- 平均値を用いるなら、ばらつきの指標は標準偏差を使う
ということを意識しましょう。
四分位範囲(IQR)の論文での記載方法

ここまでで四分位範囲がどんなものなのか、理解できたかと思います。
じゃあその四分位範囲が論文中に使われるとすると、記載方法はどうすればいいのでしょうか。
実際の論文を参考にしてみてみましょう。
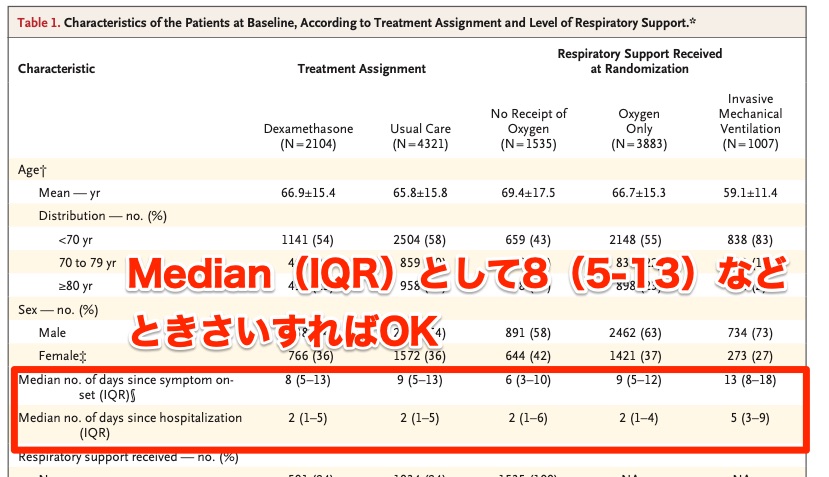
上記の通り、Median(IQR)として数値を書けばOKです。
IQRとはInterquartile Rangeの略で、四分位範囲の英語表記です。
IQR(四分位範囲)は25%点〜75%点でしたので、括弧内は(25%点-75%点)と記載すればOKですね。
四分位範囲に関してまとめ

いかがでしたか?
今回の記事では「四分位範囲とは?箱ひげ図との関連や論文お記載方法までわかりやすく解説」ということでお伝えしました。
- 四分位範囲とはそもそもどういったことを示しているの?
- 四分位範囲と箱ひげ図との関係は?
- 四分位範囲は何のために使われる?
- 四分位範囲を実際に論文で記載する方法は?
といったことが理解できたのなら幸いです。













コメント