「データを解析してください」と言われたら、真っ先にイメージするのは「平均値を計算してみる」ということではないでしょうか?
それぐらい、統計=平均値、というイメージが皆さんの頭の中に存在しているように思えます。
それはある意味正解で、ある意味不正解です。
平均値は、統計解析をする上で重要な代表値であることは間違いありません。
ですが、平均値だけでは統計を知っている、とは言えませんね。
この記事では、統計でとても重要な平均値に関して簡単にわかりやすく解説します。
この記事を読めば、このようなことがわかるようになります。
- 平均値の公式は?わかりやすく言葉で解説
- 平均値と同じぐらい統計では重要な中央値について
- 平均値と中央値が違った場合にどうする?
- 平均値と中央値をエクセルで計算する方法
それでは早速いってみましょう!
平均値とは?意味や特徴などどんな場面で有効な指標なの?

「データを要約する」といった場合に、ほとんどの人は「平均値を出力する」ことから始めると思います。
それはそれで間違いないことです。
平均値を出す、ということは、立派な統計解析です。
しかし、一つだけ難点があります。
それは「平均値”だけ”を計算するのでは不十分」ということ。
なぜなら、平均値がその効力を発揮する場面というのは、「データの分布が左右対称」である場合です。
左右対称のデータ分布で、一番有名なのが正規分布です。
例えば、身長のデータは正規分布に従うことが知られています。
正規分布のような左右対称の分布の場合、平均値はデータの真ん中に近くになります。
下記のグラフが正規分布です。
この場合、平均値は山の頂点に近い値になります。
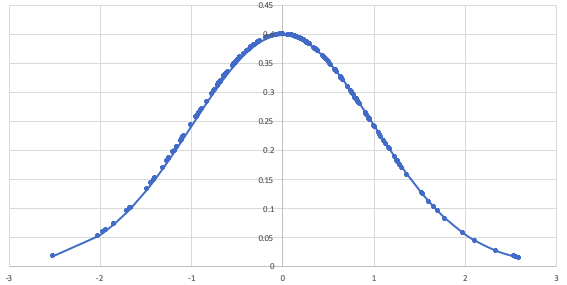
重要なので、もう一度書いておきますね。
ぜひこの特徴は覚えておいてください!
平均値の公式を簡単にわかりやすく!
ここで統計のサイトっぽく、平均値の公式を載せておきます。
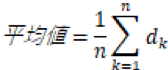
余談ですが、やはり統計に苦手意識を持つ原因の一つが「数式記号」だと思います。
数式記号の意味するところが分からなくなり、調べるだけで一苦労。
統計の勉強をしているのか、数式記号の勉強をしているのか分からなくなって嫌になってしまいます。
実際に私がそんな一人でした。
なので、平均値を数式記号を使わずに、表現しますね。
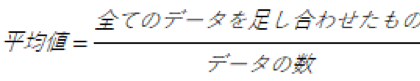
平均値は一つだけじゃない。それぞれの特徴とは
平均値といえば算術平均をイメージする方が大半だと思います。
この記事でも、平均値=算術平均として記事を書いています。
しかし、実は平均値にも様々な種類があるのです。
- 算術平均:上記で記載した平均値です。
- 幾何平均:全てのデータの値を掛け合わせて、データ数の累乗根を求めた値です。
- 調和平均:逆数の算術平均の逆数です。
この中で、医薬品開発によく使われる平均値は、算術平均と幾何平均です。
調和平均は見たことがありません。
幾何平均は、分布が右裾を引いている場合に有効です。
右に裾を引いている分布のことを対数正規分布と呼びます。
対数正規分布の特徴は、データを対数変換することで正規分布に近づくということ。
そして、幾何平均とは、対数変換後のデータにおける算術平均と同じ意味です。
平均値が相応しくない場合には中央値を使う!違いとは?

平均値は、統計解析で重要な指標であることを学びました。
では逆に、平均値が代表値として相応しくない場面はどのような場合でしょうか?
それは”平均値がふさわしい場面”の反対なので「データの分布が左右対称でない場合」です。
例えば、臨床検査値(ASTやALTなど)は左右対称の分布ではないことが知られています。
臨床検査値は、少数のデータが非常に大きいデータになることがあり、右裾を引いた分布になっています。
先ほど出てきた対数正規分布ですね。
下記が対数正規分布です。
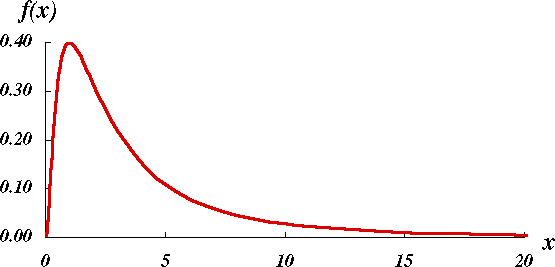
対数正規分布の場合には、少数の大きなデータに引っ張られて平均値は大きくなります。
そのため、平均値は分布の山より右側に寄ることになります。
このように左右対称の分布ではない場合には、中央値が代表値としてふさわしいです。
平均値と中央値の違いは?それぞれの特徴
具体例を用いて、平均値と中央値の特徴をまとめてみたいと思います。
5人の小学生がいて、あるテストの点数が 30 点、40 点、50 点、60 点、70 点だったとき、平均値はどうなりますか?
この問題。
簡単に解けますよね。
(30+40+50+60+70)÷5=50 点、となります。
では、中央値はどうでしょうか。
中央値は真ん中(3 つ目)の値である 50 点となります。
このケースでは平均値と中央値が同じになりました。
では、次の場合はどうでしょう。
5人の小学生がいて、あるテストの点数が 30 点、35点、40点、40 点、90 点だったとき、平均値はどうなりますか?
平均値は(30+35+40+40+90)÷5=47 点となり、90 点以外の4人は平均値以下です。
中央値は、真ん中の値ですので 40 点となります。
このように、平均値の場合は他の値と比べて極端に高い(もしくは低い)値があることによって、影響を受けてしまいます。
中央値の場合は、真ん中の値ですので、そのような影響は受けません。
平均値と中央値の差が大きいなら左右対称ではない
そこからわかることは、当たり前ですが、中央値はどのようなデータであってもその真ん中を示すということ。
そして、上記の例の通り、極端な値に全く影響を受けません。
一方の平均値は、左右対称のデータであればデータの真ん中付近になりますが極端な値があった場合にはその値に引っ張られた値になります。
つまり、以下のようなことを知ることができます。
- 左右対称の分布の場合、最頻値=中央値=平均値となります。
- 右に裾を引く分布の場合、最頻値<中央値<平均値となります。
- 左に裾を引く分布の場合、最頻値>中央値>平均値となります。
この性質を知っていると、平均値と中央値を見ると以下のようなことが分かります。
平均値と中央値が同じような値を示している場合には、そのデータが左右対称の分布になっている。
平均値と中央値が異なる値を示している場合には、そのデータが左右対称の分布になっていない。
かなり重要な性質なので、これも覚えておきましょう!
要約統計量を出力するときには、平均値と中央値をセットで出力する
平均値と中央値にはかなり違いがあることがわかりました。
そのため、実際にデータを要約する際には、中央値と平均値をセットで出力することが有益です。
平均値と中央値が異なる場合どうすればいい?

平均値と中央値が異なる場合、データの分布が左右対称ではないことがわかりました。
では実際には、平均値と中央値が異なる場合にどういった処理をする必要があるのでしょうか?
これは一概には言えませんが、多くの場合、変数変換をすることを検討する可能性があります。
変数変換をすることで、データの分布が左右対称に近づくことがあるからです。
例えば先ほど例に挙げた、臨床検査値のような右裾を引いたデータは「対数正規分布」と呼ばれます。
なぜ対数正規分布と呼ばれるかというと、データを対数(Log)変換すると、正規分布に従うという性質があるからです。
正規分布に従えば、データの扱いがかなり楽になります。
平均値を算出することがOKになりますし、T検定のようなパラメトリックな検定を実施することも可能になります。
中央値の方が扱いやすい気がするけど…
ここまでしっかり解説を読んでいただいている方は、恐らくこのように思うのではないでしょうか。
データ解析をする際には、常に中央値を出せばよいのでは…
私も一時期、そのように思っていました。
確かに、中央値はどのようなデータでも同じように解釈が可能であるため、かなり便利な指標です。
しかしそれでも平均値を出すことが有益であることがあるのです。
それは、統計学的検定の話と絡みます。
要するに、パラメトリックな検定の一つであるT検定では、平均値をベースにして検定を実施していますし、多くの解析で正規分布が前提としているためです。
このような理由から、平均値を要約統計量として出力することは大変意味のあることなのです。
エクセルで平均値と中央値を算出する
平均値と中央値がわかったところで、エクセルではどんな関数を使えばいいのか?という話です。
まずは結論から。
- エクセルで平均値を算出する関数は「=average()」です。
- エクセルで中央値を算出する関数は「=median()」です。
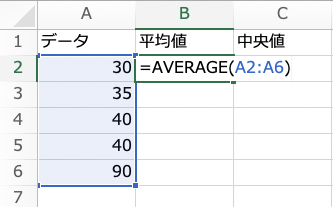
実際に、先ほどの5人の小学生がいて、あるテストの点数が 30 点、35点、40点、40 点、90 点だったときの平均値と中央値をエクセルで算出してみます。
平均値はこのように「=average(A2:A6)」とすれば47が出てきます。
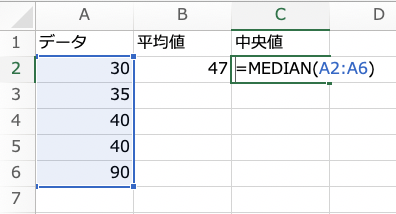
中央値はこのように「=median(A2:A6)」とすれば40が出てきます。
平均値の特徴を知れば数値の解釈に気をつけなければならない場面がわかる
平均値はかなり有名で、統計を知らなくても平均値だけは知っている方も多いと思います。
しかし、前述の通り平均値は左右対称の分布の場合に有効であり、それ以外では誤用しているということになります。
誤用の例として、平均結婚年齢というものをみてみましょう。
平均という言葉に騙されてはいけない!
平均結婚年齢というものがあります。
文字通り、結婚する年齢の平均値のことですね。
2016年現在での女性の平均結婚年齢は、おおよそ30歳です。
私の周りでは、このような会話を聞くことがあります。
「ちょうど平均結婚年齢になったけど、まだ大丈夫!」
これを聞いたとき、みなさんはどう思いますか?
結婚できる年齢の分布を考えてみる
平均値と中央値を学んだ皆さんの中には、「あれ?」と気づく方もいらっしゃるのではないでしょうか。
そう、結婚年齢の中央値はもっと若いところにあるのです。
女性が結婚出来る下限は16歳です。
ですが上限はなく、40代でも50代でも結婚できます。
するとどうなるでしょうか?
年収の分布と同じように、右側に外れ値が出てくる分布になっていないでしょうか?
つまり、平均結婚年齢は、40代や50代に引っ張られている可能性があるのです!!
平均値と中央値の違いに関するまとめ

- 要約統計量を出力する際には、平均値と中央値を両方ともに出力することが望ましい。
- 平均値と中央値を確認することで、そのデータが左右対称の分布であるかが分かる。
- 平均値と中央値が異なる場合には、変数変換(例えば対数変換など)を検討する必要がある。
そして、平均値の算出がふさわしい正規分布かどうかを視覚的に判断するのにヒストグラムというグラフ化がとても重要ですので、合わせてご確認ください。
また、中央値に対応するグラフに箱ひげ図というものがありますので、そちらも合わせてご確認ください。
統計に関するご質問があれば、メルマガにご登録の上ご質問くださいませ!














コメント
コメント一覧 (4件)
[…] […]
[…] 平均値や中央値、標準偏差などですね。 […]
[…] そして、平均値や分散を要約した値という意味で、「要約統計量」といいます。 […]
[…] 正規分布は平均値と標準偏差(SD)が決まると、その形が一つに決まります。 […]