この記事では「標準化差とはどんな定義でどこで使う?SMDの略や計算方法もわかりやすく!」ということでお伝えします。
- 標準化差ってどんな定義?
- 標準化差を使う目的は?
- 標準化差は論文でどう使われているの?
といったことがわかるようになります!
標準化差とは?医療統計ではどんな状況で使われる指標なの?

まずは標準化差について、どんな状況で使われる指標なのかを整理します。
現状、標準化差は傾向スコアマッチングなど、傾向スコアを用いた解析をしている論文でよく見かける指標です。
傾向スコアマッチングとは、すでにあるデータに対して、背景情報が似たような被験者をマッチングさせ、マッチングできたデータだけで解析を実施する統計手法。
標準化差は傾向スコアマッチングした後の背景情報が揃っているかどうかの指標
じゃあ標準化差は傾向スコアマッチングでどんな目的で使われているのでしょうか。
それは、傾向スコアマッチングした後の背景情報が揃っているかどうかの指標として使われています。
背景情報の比較で、P値を用いている論文をよく見かけませんか?
しかし群間のバランスをP値で評価するのは適切ではない、という意見が主流になってきています。
(私も背景情報はP値で評価しない方がいい派です。)
特に傾向スコアマッチングは、背景情報を揃えることを目的とする統計手法のため、群間で背景情報は揃う、という前提です。
となると、P値を用いる統計的検定では「違いがない(同じである)」ということを示すことができないため、傾向スコアマッチングを用いる目的を考えても、P値は適切ではありません。
また、P値はサンプルサイズに依存するため、例え群間で背景情報が揃っていても、大規模な観察研究であればマッチングした後でも有意差が出ることはあるでしょう。
以上を理由として、P値に依存しない数値化が欲しい、という目的で標準化差が用いられるようになりました。
標準化差の定義と論文での使い方は?SMDってなんの略?

標準化差の目的が理解できたところで、次は標準化差の定義を見てみましょう。
標準化差の定義は以下の通りです。
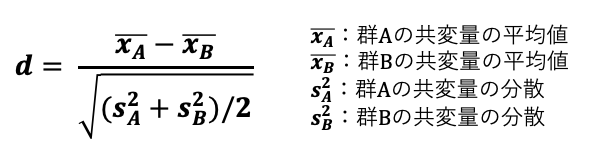
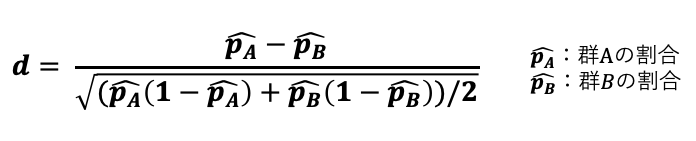
数式自体は全く覚える必要ないですが、一度だけ数式の分子に着目していただければと思います。
分子は「群間の平均値の差」や「群間の割合の差」を示しているため、群間の平均値の差・群間の割合の差が小さければ標準化差は小さい値になる、ということがわかります。
そして標準化差の見方としては「標準化差の絶対値が0.1より小さければ群間でバランスが取れている」とされる目安です。
絶対値が0.1を超えているから絶対にダメだ、という訳ではないですが、一つの目安として使っていただければと思います。
標準化差の論文での使われ方は?SMDは何の略なの?
標準化差の定義がわかったところで、論文での使われ方も見てみましょう。
繰り返しになりますが、標準化差は傾向スコアマッチングでつかわておりますので、論文では傾向スコアマッチングした後の背景情報の表に加えることが多いです。
例えば下記の論文ではこのように表にしています。

標準化差は英語で「Standardised Difference」と呼ばれていますので、上記のような書き方がなされています。
また、連続量の場合には「Standardised Mean Difference (SMD)」と表記されることもあります。
どちらも同じ「標準化差」を示していることには変わらないです。
実際に標準化差を算出するには?
では最後に、実際に標準化差を算出するにはどうしたらいいのでしょうか?
実は簡単に実施可能なんです。
私は下記に紹介する書籍をもとにRで簡単に実施可能でした。

プログラミングコードなども細かく紹介されていますので、この本の通りに実施すれば、簡単に標準化差を算出することができますよ!
標準化差についてまとめ

いかがでしたか?
この記事では「標準化差とはどんな定義でどこで使う?SMDの略や計算方法もわかりやすく!」ということでお伝えしました。
- 標準化差ってどんな定義?
- 標準化差を使う目的は?
- 標準化差は論文でどう使われているの?
といったことがわかったのなら幸いです!
動画でも標準化差に関して解説していますので、併せてご確認くださいませ。













コメント