中央値（メジアン）は奇数と偶数の場合で求め方が違う？エクセル関数などもわかりやすく

あなたは、中央値（メジアン、メディアン）の求め方がわからない・・・というような悩みを持っていませんか？

確かに、平均値よりはマイナーな存在。

学校でちゃんと習った記憶もない。

だから、社会人になって悩む人も多いです。

 

ですが、中央値は全く難しくありません！

実は、平均値よりもはるかに簡単。

だって、言葉通り「真ん中の値」が中央値だから。

何もむずかしくないんです。

でも、何の真ん中なんだろう？っていうのがわからなくて、悩んでいる人が多い印象です。

 

このページでは、そんな中央値について。

このページを見れば、このようなことがわかるようになります。

 

 

では早速いってみましょう！

 

中央値（メジアン、メディアン）の求め方が奇数と偶数の場合で違う？

中央値は、３ステップで求めることが可能です。

その３つは、これ。

 

1. データを小さい順に並べる
2. データの数が偶数か奇数かを把握する
3. 真ん中の値を見つける

 

たったこれだけです。

では、例を見ながら一緒に解いてみましょう！

例題：あるクラスの、６人の英語の得点は６４点、５３点、８８点、５８点、９４点、７１点だった。この時の中央値を求めなさい。

この問題を、前述の通りの３ステップで中央値を求めてみましょう。

ちなみに、先に正解を記載しておきますね。

正解：中央値は６７．５点である

どうですか？

正解しましたか？

 

中央値の求め方１：データを小さい順に並べる

最初のステップは、データの並べ替え。

左から、英語の点数が悪い順に並べてみましょう。

すると、こんな感じになります。

 

５３

５８

６４

７１

８８

９４

 

ここまでは難しくないですね。

 

中央値の求め方２：データの数が偶数か奇数かを把握する

次は、データの数を把握します。

なぜかというと、偶数か奇数かで、データの真ん中の定義がちょっと違ってくるから。

今回の例だと、例題にすでに６人と記載されているので、偶数であることは明らかですね。

念の為数えてみても、データの数は６個です。

ということで、データの数は偶数であることが確認できました。

 

中央値の求め方３：真ん中の値を見つける！偶数の時の求め方は？

では、最後のステップ。

真ん中の値を見つけること。

じゃあ、今回の６人のデータの真ん中はどこでしょうか？

 

・・・もしかしたら、ここでつまずいたかもしれませんね。

 

なぜなら、今回のデータの数は偶数です。

真ん中ってどこ？

って思いませんでしたか？

３番目のデータ？４番目のデータ？どっち？

って感じです。

 

そうなんです。

ここが中央値に関する注意点ですね。

 

そのため、データの数が偶数の場合の中央値は以下の定義になります。

 

となると今回の例題の場合、中央値は３番目のデータである６４点と、４番目のデータである７１点の平均値、ということになります。

なので、（６４＋７１）/２＝６７．５になるということ。

 

では、データの数が奇数の場合は？というと、これは真ん中の値が１つだけになるため、全く問題なく中央値が求められます。

 

中央値（メジアン、メディアン）はエクセルでどんな関数？実行した結果と比較！

念の為、答え合わせとして、エクセルで中央値がどうなるかを示しておきます。

エクセルの中央値算出の関数はわかりますか？

平均値と中央値の違いは？という記事でもありましたが、中央値を算出するエクセル関数は「=median(データの範囲)」ですね。

 

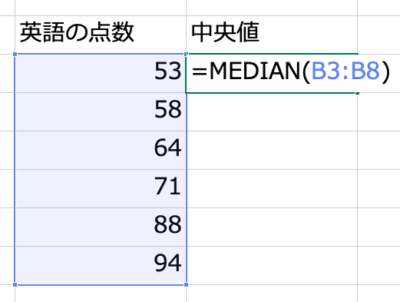
すると、このような結果になりました。

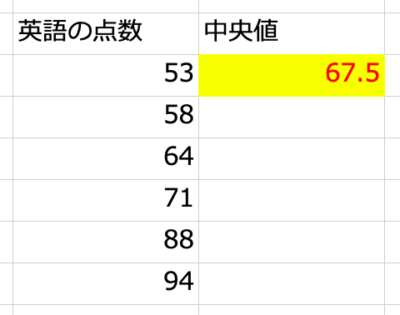
私たちが計算した中央値と一緒になりましたね。

 

中央値は外れ値に影響を受けないため、すごく便利

中央値の求め方はすごく簡単でした。

では次に考えることは、中央値はどんな場面で使うことができるか？ということです。

 

平均値は極端なデータである「外れ値」にとても影響を受ける性質がありました。

そのため、データが正規分布である時にとても有効な指標です。

逆に言えば、データが正規分布ではない時には、少々解釈に注意が必要なのが平均値でした。

 

じゃあ中央値はどうか？というと、「外れ値に全く影響されない」です。

なので実は、中央値はどんな時にでも使うことができる、とても便利な指標なのです。

 

 

中央値に対応するバラツキの指標は？

最後は、中央値に対応するバラツキに関して解説します。

その前に、平均値に対応するバラツキの表し方は、大丈夫ですか？

そう、分散や標準偏差ですね。

じゃあ中央値はどうですか？

最初に答えを示すとこうなります。

 

 

中央値は別名、50%点とも言われます。

全データの中央の値だから、全体の50%の点だ、という意味ですね。

ということは、他にも〇〇%点があって良いと思いませんか？

 

実はあるんです。

有名なのが、25%点と75%点。

25%点は、最小値と中央値の真ん中の値。

75%点は、中央値と最大値の真ん中の値です。

そして、この25%点〜75%点までの範囲を「四分位範囲」と呼びます。

データを四分割した時の範囲、という意味です。

 

黒い丸１つ１つがデータを示しているとして、上の方が大きい値、下の方が小さい値の時。

四分位範囲とは、以下のようになります。

 

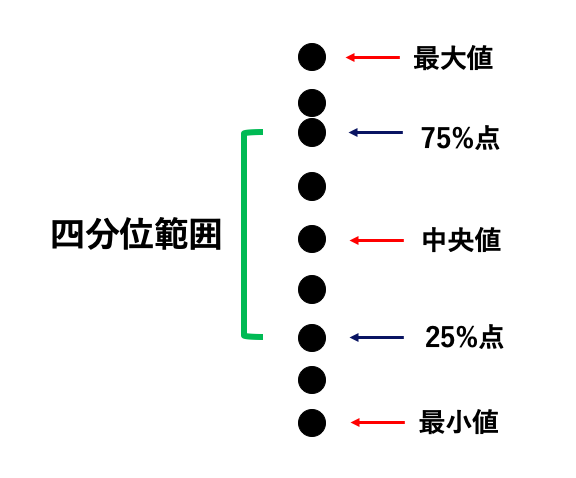
この四分位範囲が、中央値に対応するバラツキの表現方法になります。

そのため、中央値を提示する際には、四分位範囲も一緒に提示したいですね。

 

中央値と四分位範囲が一目でわかる便利なグラフが箱ひげ図

中央値と四分位範囲がわかったところで、これらが一瞬でわかる便利なグラフがあることを知っていますか？

そう、箱ひげ図です。

箱ひげ図は、中央値と四分位範囲が一目でわかる便利なグラフですので、その作成方法はぜひマスターしておきましょう。

 

中央値に関するまとめ

中央値は３つのステップで算出可能でした。

1. データを小さい順に並べる
2. データの数が偶数か奇数かを把握する
3. 真ん中の値を見つける

そして、中央値は外れ値の影響を受けないため、どんな場面でも使用可能です。

中央値に対応するバラツキの表現方法は、四分位範囲でした。