今回の記事では、EZRで多変量解析の一つであるCox比例ハザードモデルを実施する具体的な手順をお伝えします。
実際のデータを解析する際には、T検定やカイ二乗検定などの単純な検定だけでなく、共変量を調整するような多変量解析を多く実施することがありますよね。
そのため、今回の記事がそのままあなたの実務に役立つと思います。
この記事では、EZRを用いて多変量解析の一つである、Cox比例ハザードモデルを実施します。
Cox比例ハザードモデルは、応答変数(目的変数)が生存時間データである場合に使える解析手法です。
では、いってみましょう!
EZRでCox比例ハザードモデルを実施するにはどんな状況であればいい?

まず重要なのが、あなたの手元にあるデータでどの種類の回帰分析を実施するのか!?ということ。
これを知らなければ、実務でデータを解析することができませんよね。
どの回帰分析を実施するのか、という判断は、実は簡単です。
目的変数がどんな種類のデータなのか、ということを考えればいいだけ。
- 目的変数が連続量:共分散分析(重回帰分析)
- 目的変数が2値データ(カテゴリカルデータ):ロジスティック回帰分析
- 目的変数が生存時間データ:Cox比例ハザードモデル
ということなので、Cox比例ハザードモデルを実施するには目的変数が生存時間データであることが必要だと理解できました。
では早速、EZRでCox比例ハザードモデルを実践していきましょう!
EZRでCox比例ハザードモデルを実施する方法
EZRでCox比例ハザードモデルを実施します。
今回は自治医科大学さんが提供しているサンプルデータの中から「Survival」を使ってみます。
いぜん、EZRでカプランマイヤー曲線を作成した時のデータと同じです。
>>Survivalデータは、こちらからダウンロードできます。
「Age」「Sex」「Disease」「Treatment」「OS」「DaysToOS」「PS2.3.4」の7種類のデータがあります。
そのため、Age(年齢)が共変量だったと仮定して、“年齢という共変量の影響を取り除き、Treatmentごとに生存時間が変わるのか”ということをやります。
では実際にやっていきましょう!
EZRにCox比例ハザードモデルを実施するためのデータを取り込む
ではここから、EZRにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
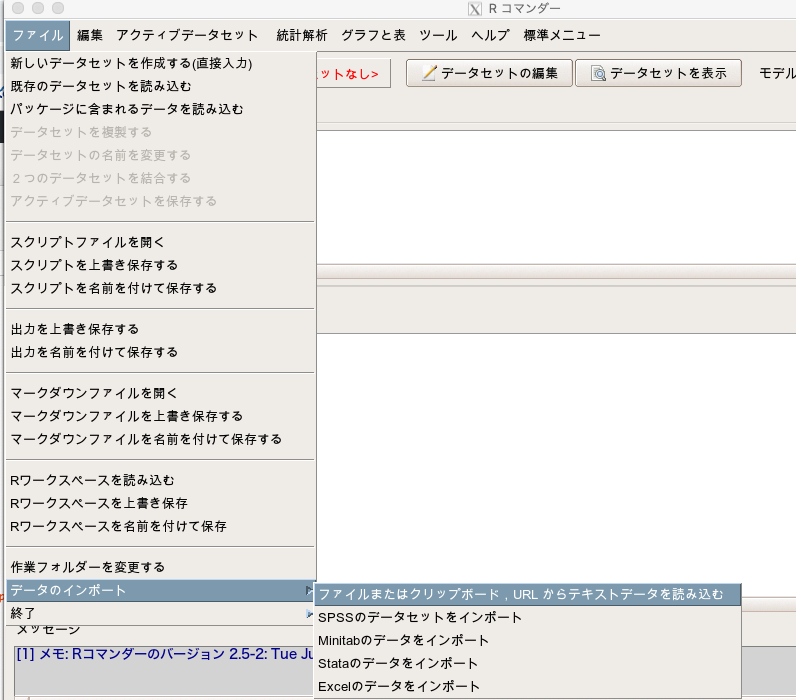
EZRを開き、「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選択します。
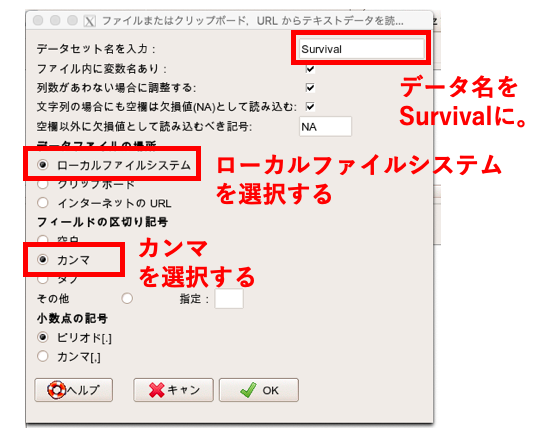
データセット名は「survival」にしましょう(実際はなんでもよいです)。
そして「ローカルファイルシステム」と「カンマ」にチェックを入れてOKを押します。
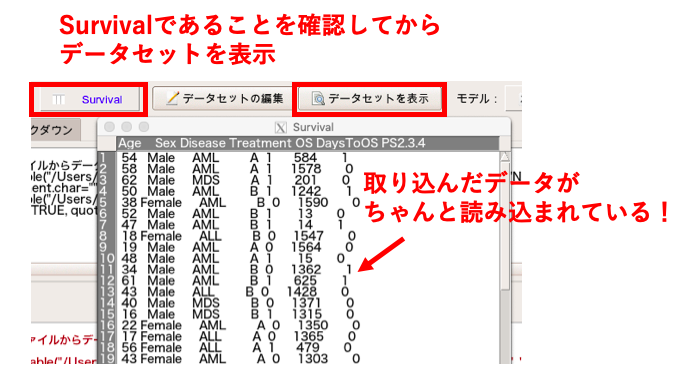
データセットが「survival」になっていることを確認し、「表示」を押してデータが正しく表示されれば取り込み完了です。
EZRでCox比例ハザードモデルを実行する!
解析するための準備が整いましたので、早速、Cox比例ハザードモデルを実施してみましょう。
Cox比例ハザードモデルを実施するには、以下の手順で行います。
「統計解析」→「生存期間の解析」→「生存期間に対する多変量解析(Cox比例ハザード回帰)」
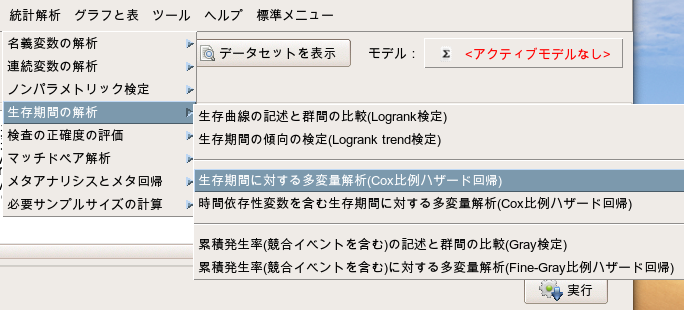
- 時間には「DaysToOS」を選択します。(変数をダブルクリックすることで選択できます。)
- イベントには「OS」を選択します。(こちらもダブルクリックです。)
- 説明変数には「Age」と「Treatment」を選択します。(こちらもダブルクリックです。)
他は、いじらなくてOKです。
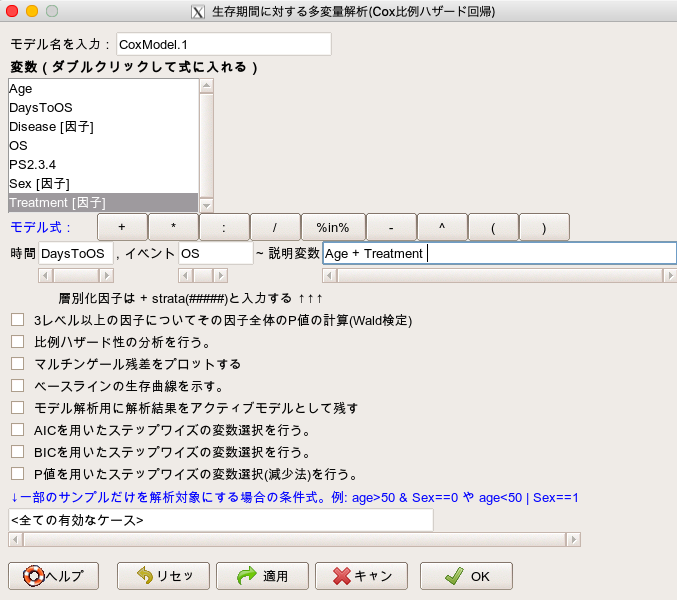
これで解析を実行すると、以下の解析を自動で行ってくれます。
- Cox比例ハザードモデルを実施した結果の表の作成
- ハザード比とその95%信頼区間に関する表の作成
EZRでのCox比例ハザードモデル結果の解釈をしよう
実際にCox比例ハザードモデルが実施できました。
では、結果の解釈をしていきましょう。
EZRで実施したCox比例ハザードモデルの結果を解釈する
まずはCox比例ハザードモデルを実施した結果の表の解析結果です。
かなりの情報量が詰まっていますね。

coxph(formula = Surv(DaysToOS, OS == 1) ~ Age + Treatment, data = survival,
method = “breslow”)
というのは、ざっくり言うと「Cox比例ハザードモデルでの解析を実施しましたよ」ということ。
そして、その回帰式が“Surv(生存期間がDaysToOS, イベントがOS)=Age+Treatment”ということですね。
解析の例数は74で、イベントは41あることも読み取れます。
重要なのが、イベントから下のこちらの部分。

ここには、説明変数で入れた「Age」と「Treatment」の結果が記載されています。
これはハザード比に関しての結果が出ているのですが、さらに下に出力されているハザード比の表の方が見やすいので、ここではちょっとスキップします。
ハザード比に関する表の解釈
次に、各説明変数のハザード比に関する結果が出力されています。

ハザード比は1だった場合に「差がない」といえます。
そのため、1から遠ければ遠い点推定値であるほど、「差がある」ということが言えます。
ここからも、有意水準が0.05だった時に有意差があるかどうかわかります。
Ageは95%信頼区間が1を跨いでいないため、有意差あり。
Treatmentは95%信頼区間が1を跨いでいないため、有意差なし。
この95%信頼区間と有意差の関係は、一目見て理解できるようになっていたいですね。
Cox比例ハザードモデルを使って単変量解析するとどうなるの?
今回も共分散分析と同様に説明変数を2つ含め、共変量の影響を除いて群間比較しました。
今回のデータでは、Ageを共変量として多変量解析を実施していましたよね。
では、共変量がなかった時に本当に結果が変わるのか!?ということをやってみましょう。
やり方の手順は先ほどと同じで、説明変数にはTreatmentの1つだけ入れます。
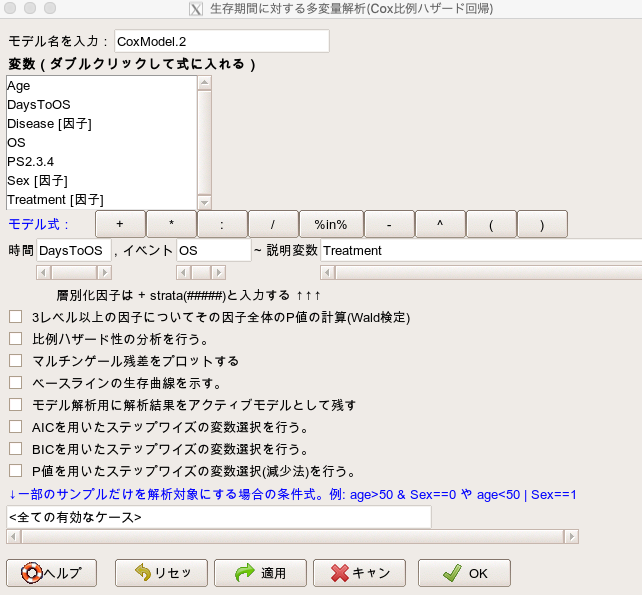
すると、下記のような結果が出力されています。

Ageで調整した場合にはP=0.6565でしたが、Ageで調整しないとP=0.09577という結果が出ました。
Ageによる調整の有無が、Treatmentの結果にかなり影響を与えていたことが分かります。
まとめ
今回は、EZRで多変量解析の一つであるCox比例ハザードモデルを実施しました。
これを実践し、結果の解釈をすることができれば、必ず実務で役に立ちます。













コメント
コメント一覧 (1件)
[…] 実際に上記のログランク検定と同じデータに対して、EZRでCox比例ハザードモデル(Cox回帰)を実施すると、以下のような結果が出力されます。 […]