母平均の検定なのに名前がややこしい分散分析。
分散分析とは、群が3群以上になったときに適用する解析手法でした。
今回の記事では、そんな分散分析をEZRで実際に解析する方法をお伝えします。
分散分析を適用する際には、正規性を確認しないといけない?
というところまで踏み込んで結果の解釈もしていきます。
有意差があった時の結論に関しても、再度復習していきましょう!
EZRで分散分析を実施するために必要となるデータを読み込む

まずは、分散分析を実施するために必要なデータを解説します。
じゃあT検定と何が違うの?というと、分散分析は群が3群以上の場合に適用する統計学的検定でしたね。
ということは、用意するデータは以下の2つを満たす必要があります。
- 母平均を検定する方法であるため、連続量のデータが必要。
- 3つ以上の群間で母平均を比較するので、3つ以上のカテゴリを持つ、カテゴリカルデータが必要。
EZRで分散分析(ANOVA)をする今回の記事で使用するデータ
ということで、今回の記事で使うデータです。
今回はA群、B群、C群の3つの群で、LDHの平均値を比較してみます。
(データは架空のデータです。)
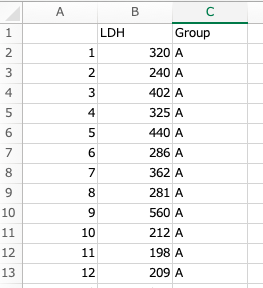
LDHが比較する値で、Groupが群を示した変数です。
A群で13例、B群で11例、C群で14例、合計38例分のデータがあります。
EZRに分散分析(ANOVA)を実施する基となるデータを読み込む
ではここから、EZRにデータを取り込みます。
まずは、サンプルデータを適切な場所に保存しておきましょう。
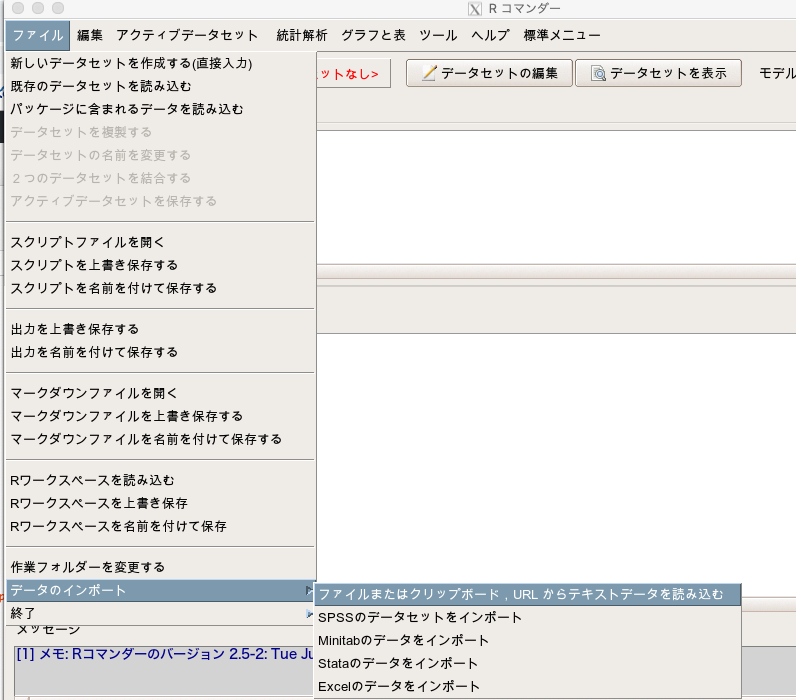
EZRを開き、「ファイル」→「データのインポート」→「ファイルまたはクリップボード, URLからテキストデータを読み込む」を選択します。
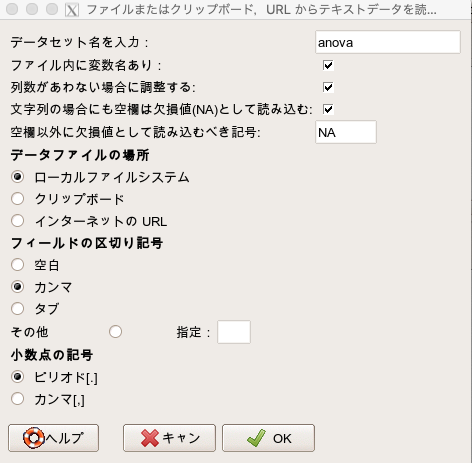
データセット名は「anova」にしましょう(実際はなんでもよい)。
そして「ローカルファイルシステム」と「カンマ」にチェックを入れてOKを押します。
データセットが「anova」になっていることを確認し、「表示」を押してデータが正しく表示されれば取り込み完了です。

EZRで分散分析(ANOVA)を実践する!
解析するための準備が整いましたので、早速分散分析を実施してみましょう。
分散分析を実施するには、以下の手順で行います。
「統計解析」→「連続変数の解析」→「3群以上の平均値の比較(一元配置分散分析one-way ANOVA)」
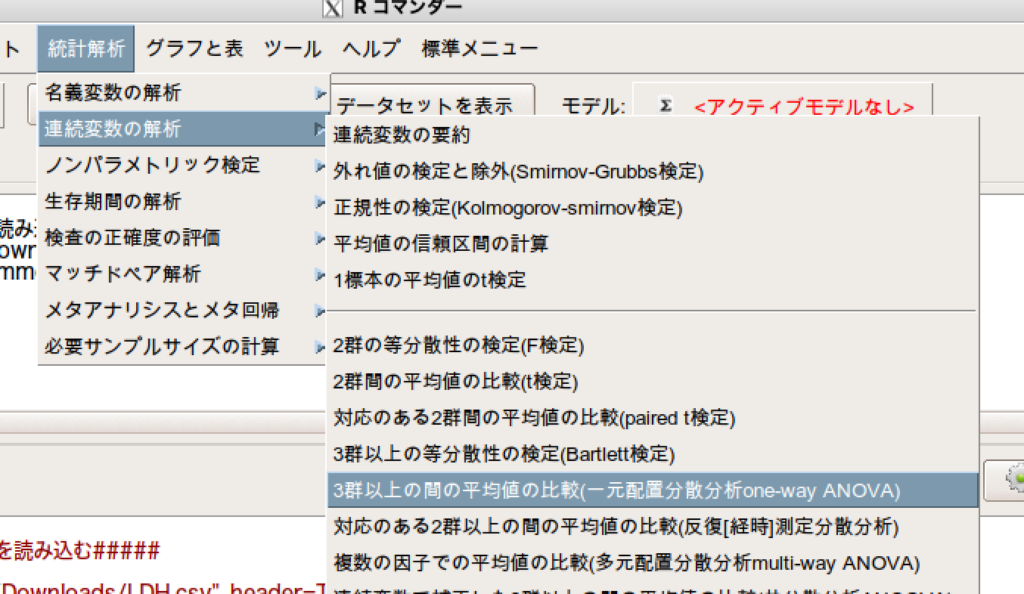
- 目的変数(1つ選択)で「LDH」を選択します。
- 比較する群(1つ以上選択)で「Group」を選択します。
- グラフは「箱ひげ」を選択します。
- 等分散と考えますか?については「はい(一元配置分散分析)」を選択します。
- 2群ずつの比較(post-hoc検定)に関しては、今回はBonferroni法を使ってみます。
他は、いじらなくてOKです。
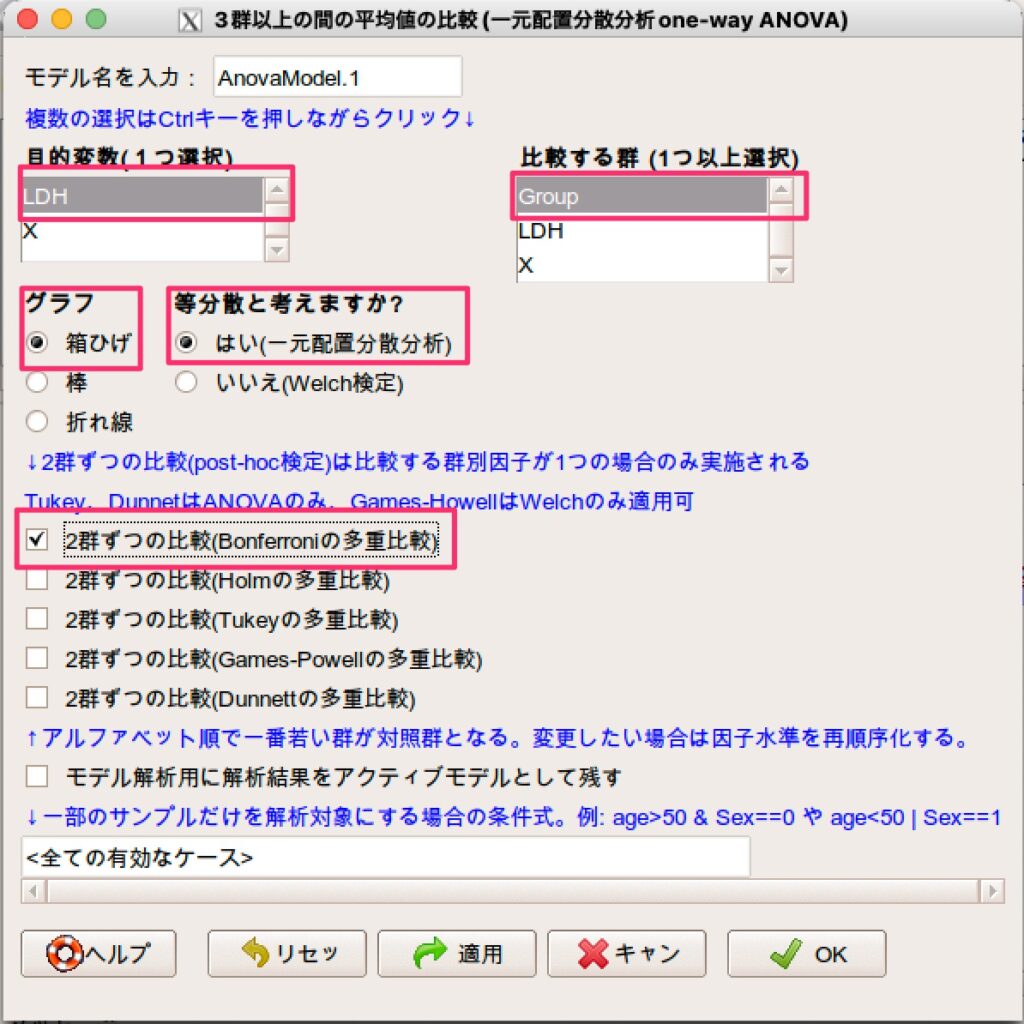
これで解析を実行すると、以下の解析を自動で行ってくれます。
- 分散分析表の作成
- 各群の平均と標準偏差の要約
- 各群の箱ひげ図の作成
- 多重性を考慮した2群比較
分散分析(ANOVA)の結果を解釈しよう!有意差あった時は多重比較結果を見る?
実際に分散分析が実施できました。
では、結果の解釈をしていきましょう。
分散分析表の結果解釈
まずは分散分析表の解析結果です。

Factor(Group)とは、要因としてGroupという変数を選択した、という意味です。
Residualsというのは、残差という意味です。
分散分析表で見るべきポイントは、自由度(Df)とP値(Pr(>F))の2つかなと思います。
- 要因(factor)の自由度は、必ず”カテゴリの数-1”です。
- 今回は、A群、B群、C群の3つのカテゴリなので、3-1=2が自由度になります。
もしカテゴリの数が4つなら、自由度は4-1=3になります。
残差(Residuals)の自由度は、”データの総数-カテゴリの数”です。
今回は、45症例分のデータで、カテゴリの数が3でした。
そのため、残差の自由度は45-3=42です。
余談ですが、統計検定2級でも分散分析表の見方は問題として頻出しますので、読み取れるようにしましょう。
P値に関しては、他の様々な統計解析結果と解釈方法は同じです。
各群の平均と標準偏差の要約の結果解釈
その次に、各群の平均値と標準偏差が要約されています。

結果のキャプチャだとわかりにくいかも知れないので、表にしておきます。
| 平均 | 標準偏差 | |
| A群 | 323.8 | 104.6 |
| B群 | 490.8 | 156.2 |
| C群 | 334.1 | 112.5 |
この結果からのP値は、P=0.00356です。
その時に、どういった結論になるかわかりますか?
帰無仮説と対立仮説を確認しましょう!
- 帰無仮説H0:A群の母平均=B群の母平均=C群の母平均
- 対立仮説H1:A群の母平均、B群の母平均、C群の母平均の中に異なる値がある
そのため今回も、A群・B群・C群のどこかの平均値が異なる、という結論になります。
EZRで分散分析(ANOVA)をすると箱ひげ図も出力される
設定の際に、グラフは「箱ひげ」を出力するようにチェックを入れたので、箱ひげ図が作成されています。
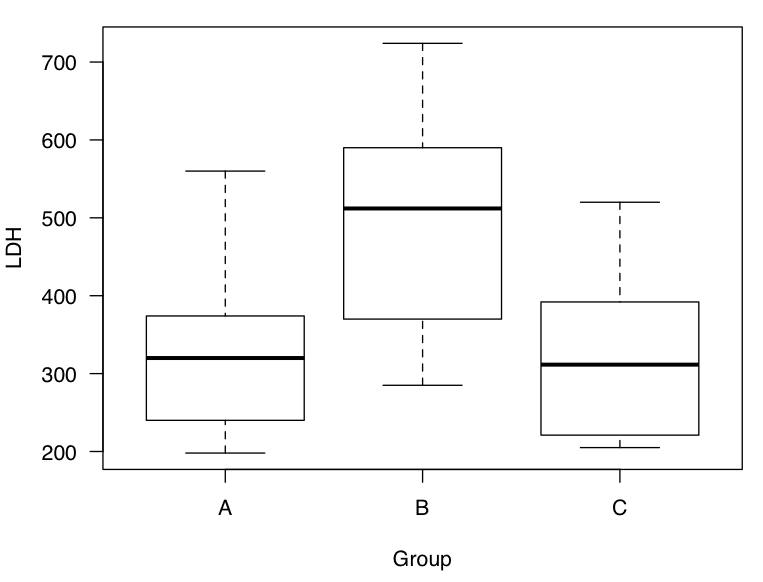
詳細は箱ひげ図の記事を参照していただきたいのですが、簡単に解説します。
箱ひげ図は、箱の部分とひげの部分がある、かなり特徴的なグラフです。
箱が四分位範囲を示しています。
ひげは箱の1.5倍(それぞれ上側に1.5倍、下側に1.5倍の意味)の長さまでのデータの範囲を示しています。
ひげから外れたデータは、外れ値として示されています。
これを見るだけでも、データの分布がA群、B群、C群で異なっていることが分かります。
EZRで分散分析(ANOVA)をすると多重性を考慮した2群比較の結果も出力される
そして、多重性を考慮した2群比較の結果も出力されています。
今回はBonferroni法を選択したため、Bonferroni法による多重性の考慮がされています。
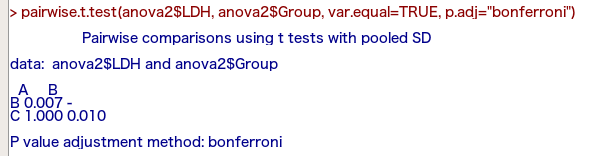
この結果のP値は、以下の通りです。
- A群 vs B群のP値:0.007
- A群 vs C群のP値:1.000
- B群 vs C群のP値:0.010
ですので、多重性を考慮したとしても、統計学的にはA群とB群の間、B群とC群の間の2つの比較で有意差がありそうです。
多重性を考慮した解析は他にもTukey(テューキー)の検定、Dunnett(ダネット)の検定が選べるので、状況に応じて選択してください。
EZRで分散分析をするのに等分散性の確認は必要か?
分散分析を実施するときに「等分散と考えますか?」に「はい」としました。
今回ご紹介した手順では、等分散性に関する確認をしませんでしたが、本当は等分散性を確認する必要があるのでしょうか?
結論からいうと、“確認は不要”です。
理由としては、得られたデータでの分散を確認しても、あまり意味がないからです。
というのも、分散分析でやっていることは「母平均」がどうかの検定。
つまり、母集団での平均がどうなっているのか、ということが興味です。
そのため、解析しているデータ、つまり標本データでいくら確認したとしても、本当に母集団が等分散かどうかは分からないのです。
今回のデータで等分散だったとしても、同じ症例数の標本をもう一度選択したときのデータは等分散ではないかもしれません。
標本の得られ方次第で、等分散だったり等分散じゃなかったりするので、得られているデータでの等分散性確認は不要です。
そして、等分散性の検定についても実施不要です。
先ほど述べた理由に加え、統計学的検定の多重性の問題が発生するからです。
以上より、等分散性の確認は不要です。
まとめ

今回は、EZRで分散分析を実施しました。
データさえちゃんと作りこめば、特に難しいことはありませんでした。
注意すべきは、有意差があった時の対立仮説と、等分散性の考え方。
ぜひ何度も確認して、理解していきましょう!














コメント
コメント一覧 (2件)
[…] 実際には、EZRで分散分析(ANOVA)を実施したデータに関してC群を削除し、A群とB群の2群だけのデータにしたものです。 […]
[…] […]