1標本問題における差の検定としてのノンパラメトリックな手法は、符号検定sign testやウィルコクソンの符号付順位検定Wilcoxon signed rank test(1標本Wilcoxon検定とも呼ばれます)があります。
(他の統計ソフトだとWilcoxonの符号付順位「和」検定とも呼ばれます。)
符号検定は差の向きだけを考慮するため、Wilcoxon符号付順位検定と比較して検出力が劣ります。
一方でWilcoxon符号付順位検定は、差の大きさも順位として考慮するので検出力が高くなります。
そのため、できればWilcoxonの符号付順位検定を実施したいですよね。
この記事では統計ソフトSPSSを使ってWilcoxonの符号付順位検定の実施方法と分析結果の解釈を行います。
Wilcoxon の符号付順位検定(Wilcoxon signed rank test)とは?

Wilcoxonの符号付順位検定(Wilcoxon signed rank test)は、対応のあるt検定のノンパラメトリック版です。
Wilcoxonの符号付順位検定の適用条件をまずは整理しましょう。
- 連続量のデータ(量的データ)であること
- 1つの標本に対して条件を変えて得た2つのデータであること(対応のあるデータであること)
ノンパラメトリックなので、条件が少ないですね。
Wilcoxonの符号付願位検定での仮説は、変数Aと変数Bを比較するとすれば、
帰無仮説H₀:Aの分布中心=Bの分布中心
対立仮説H₁:Aの分布中心≠Bの分布中心
という仮説を立てて、検定します。
SPSSによるWilcoxonの符号付順位検定
では早速、SPSSでWilcoxonの符号付順位検定を実施していきましょう!
使用するデータは、SPSSをダウンロードするとサンプルデータとしてついてくるdietstudy.savです。
このようなデータですね。
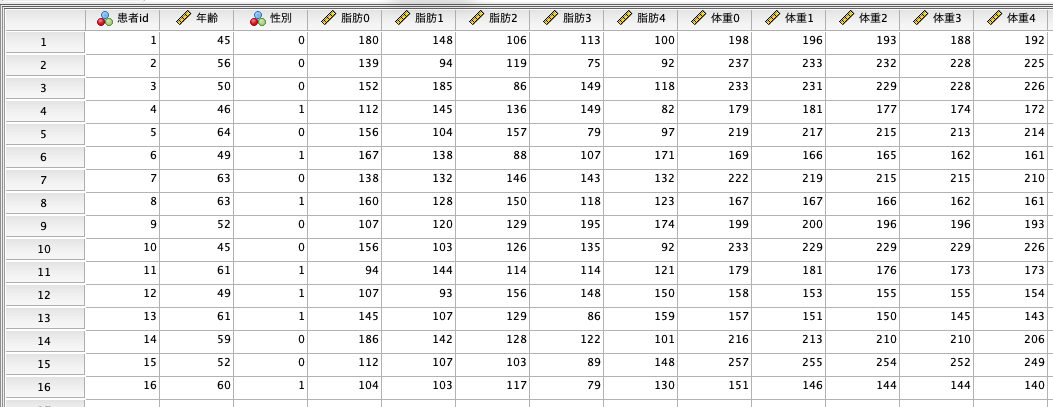
今回の記事では、ベースラインの体重(体重0)と最終時点の体重(体重4)を比較していきます。
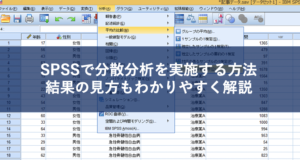
まずメニューから[分析(A)]→[ノンパラメトリック検定(N)]→[対応サンプル(R)]を選びます。
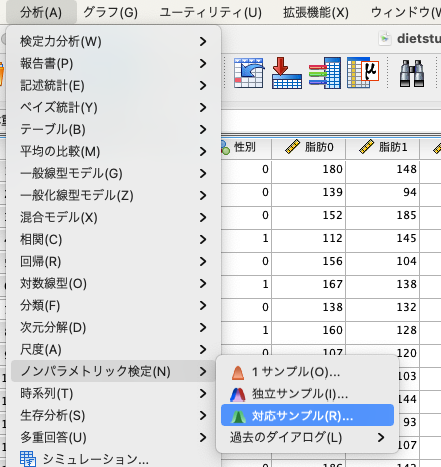
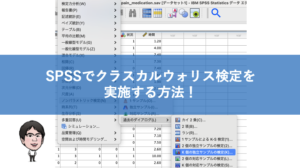
次に、下記のダイアログボックスが現れるので、[フィールド]タブをクリックし、比較したいデータを[検定フィールド]に移動させます。
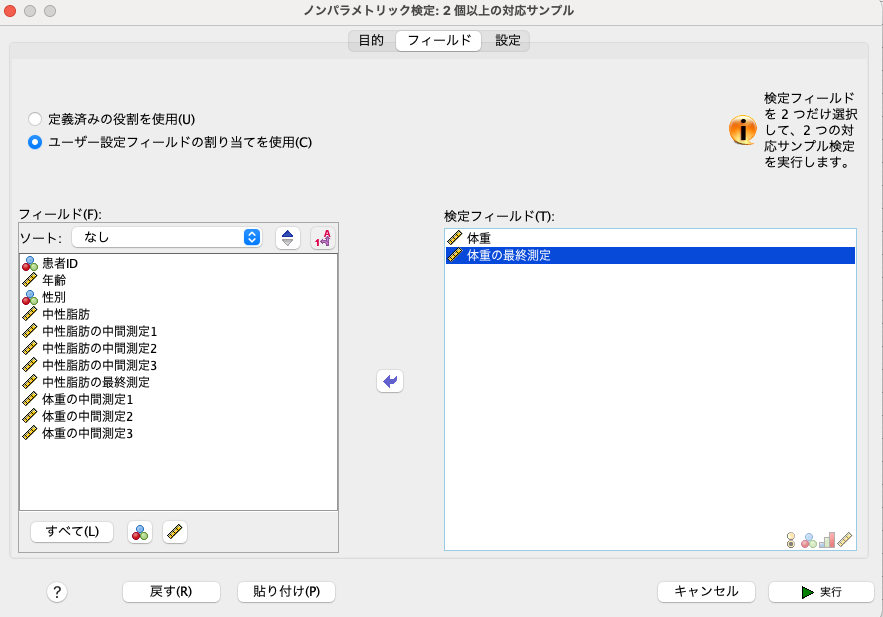
その後、[設定]タブをクリックして、[検定を選択]を選びます。
そして、[検定のカスタマイズ(C)]をクリックして、 [Wilcoxon一致するベアの符号付き順位(2サンブル)(W)]にチェックを入れます。
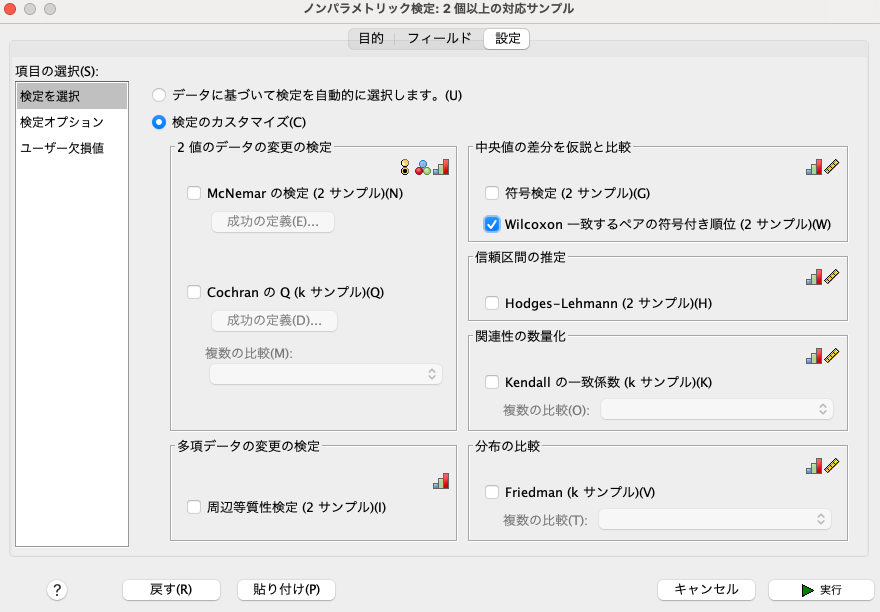
その後に、実行をクリックすると結果が出力されます。

ちなみに、[設定]タブをクリック~[Wilcoxon一致するベアの符号付き順位(2サンブル)(W)]にチェックを入れるまでの手順は省略しても構いません。
SPSSによるWilcoxonの符号付順位検定の結果の読み方
再度、結果を掲載します。

ここで注目すべき点は有意確率(P値)です。
この有意確率(P値)が事前に設定した有意水準(0.05や0.01)未満だと有意差ありということになります。

ここではp<0.001であり、有意水準0.05に対して有意な差が見出された、ということになります。
ノンパラメトリックな手法の基本的な要約統計量
ノンパラメトリックな手法を行ったときの要約統計量は、中央値と四分位範囲を述べるべきだとされています。
医学論文では、ノンパラメトリックな手法を行っても平均と標準偏差を提示することが多いですが、データが正規分布に従っていないのであれば、平均と標準偏差の情報は役に立たないことを理解しておく必要があります。
まとめ

この記事ではSPSSでWilcoxonの符号付順位検定を実施する方法をお伝えしました。
対応のあるノンパラメトリックな検定ということで、適用条件は以下の二つでしたね。
- 連続量のデータ(量的データ)であること
- 1つの標本に対して条件を変えて得た2つのデータであること(対応のあるデータであること)
ぜひ結果の解釈までご自身でできるようになっていきましょう!










コメント