中心極限定理と大数の法則の関係は？二項分布でも得られた平均値が正規分布する？

今回の記事では、中心極限定理についてお伝えします。

中心極限定理は、統計の教科書などに必ず出てくる知識ですよね。

でも、なかなかどんな定理なのか分からない。。。。

しかも、同じような言葉として大数の法則も。

中心極限定理と大数の法則との違いや関係は？？？？

そんな疑問が解決するようになりますよ！

 

中心極限定理とは？

中心極限定理をもう少し厳密な言い方で表現すると以下のようになります。

中心極限定理から導かれる結果として、どんな分布をする集団でも半ば強引に正規分布にしてしまえるという性質は、統計学において極めて重要。

ノンパラメトリック (確率分布に関するパラメータを使わない) 検定の多くも統計量が漸近的に正規分布することを利用しているのです。

 

中心極限定理は母集団には成り立たないことに注意！

ただし注意しなくてはいけないことが一つ。

中心極限定理が意味することは、標本数が大きくなると標本の分布型によらず、母集団の平均値は正規分布するということではありません。

いくらたくさん標本をとったととしても、ランダム標本を元に戻しながら繰り返して抽出した場合（復元無作為抽出）には、母集団の性質が変わることはない。

母集団と標本の知識は重要ですね。

 

中心極限定理が意味することは、どんな母集団からでも無作為抽出され標本サンプルを整理して作った標本平均の分布が正規分布に近づくということ。

たとえば一様分布する母集団や二項分布する母集団から標本を得る場合も、母集団が変化することではなく、その標本の平均値が正規分布に従うということ。

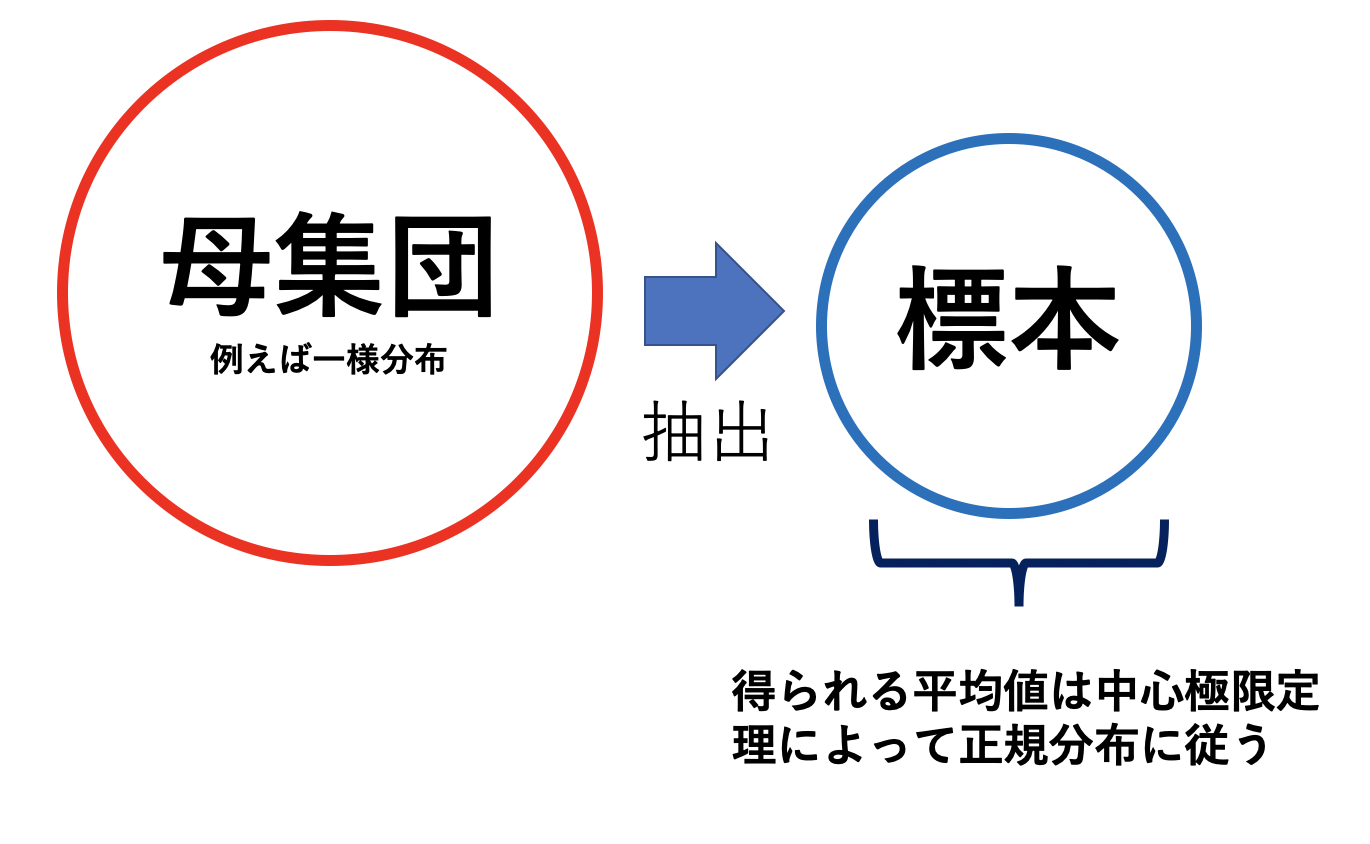
それにしても、元の分布が何であれ、そこからサンプリングされた標本の平均値が正規分布に従うということは、ちょっと不思議な感じがしますよね。

 

中心極限定理が成り立つための条件

ところで、中心極限定理が成り立つための条件については、リンデベルグ、レビィ、リアプノフ達が非常に詳しく研究している。

それによると、中心極限定理が成り立つためには分布が平均と分散をもつことが必要とされまる。

たとえば、平均や分散をもたないコーシー分布では中心極限定理が成り立たないことに注意。

逆に、確率分布が平均と分散をもちさえすれば、互いに独立な小さな誤差の集積した結果は、平均と分散以外の微細構造にはよらずに漸近的につねに正規分布にしたがうのです。

ただし、中心極限定理が成り立ち正規分布に従うとはいっても、正規分布への収束の速さとタイプはさまざまで、一般に左右非対称の分布では収束は遅いです。

 

中心極限定理と大数の法則との関係

大数の法則は、あるデータから求められた経験的な期待値と真の期待値の誤差は、データ数が増えるにつれて小さくなるという法則です。

別の言い方をすると、標本の数が増えれば増えるほど、ある事象が発生する割合（経験的頻度）は、一定の値に近づき、その値は事象の発生する確率（先験的確率）に等しい。というものです。

 

大数の法則はどこで使われている？

大数の法則は、年金数理や保険数理の分野の基礎法則となっています。

 

たとえば、死亡率が10,000分の1の集団があったとしましょう。

この集団の人数が、仮に10,000人だったとすると、死亡する人数の期待値は1人ということになりますが、実際には、3人死亡するかも知れないし、誰も死なないかもしれない。

前者の場合、死亡した人の割合は死亡率の3倍の10,000分の3で、後者の場合はゼロです。

どちらも死亡率には一致しませんが、死亡者が1人のときだけ、死亡する割合が死亡する確率に一致します。

 

では、この集団が1,000万人になると死亡者の期待値はいくらでしょうか。

1,000人ですよね。

ここまで人数が増えると死亡者が増えても減っても、その差はせいぜい数十人くらいにとどまり、よっぽどのことがない限り、実際の死亡者が倍の2,000人になったり、ゼロだったりすることはありません。

すなわち、標本の人数が増えることによって、死亡する割合が死亡率である1,000分の1に近づいていくのです。

逆に死亡率がわからないときでも、この大数の法則を利用すれば、死亡率を推定することができます。

 

このように、生命保険料の計算のもととなる死亡率は大数の法則を利用して求められるのです。

 

大数の法則には大数の弱法則と大数の強法則の2種類ある

実は大数の法則には、大数の弱法則と大数の強法則の２種類あるんです。

どの面も同様に確からしい確率 1／6 であるような6面サイコロ投げを例に考えてみる。

1の目がでたときの確率変数を 1 、それ以外を0とすると、サイコロ投げによって得られる確率変数Xの値は1か0になる。

このサイコロ投げを非常に無限回投げるというゲームを1回の施行と考え、そのゲームを多数回行う。

1回目のゲームで得られる確率変数を X11、X21、・・・、Xn1、・・・とする。

2回目のゲームで得られた確率変数も X12、X22、・・・、Xn2、・・・とし、X11、X21、・・・、Xn1、・・・、X12、X22、・・・、Xn2・・・、X1m、X2m、・・・、Xnm、・・・と多くの試行をする。

 

ここで各ゲームにおける、n 回目までに表が得られる相対度数を、

Xn1（平均）=（X11、X21、・・・、Xn1）／n

Xn2（平均）=（X12、X22、・・・、Xn22）／n

・・・

Xnm（平均）=（X1m、X2m、・・・、Xnm）／n

とする。

 

このようにして集められた非常に多くの Xn1（平均）、Xn2（平均）、Xnm（平均）・・・の中には 1／6 から大きく外れるものもまれにはあるが、その確率は非常に小さいというのが大数の弱法則である。

これに対して、 各ゲーム毎に計算される量 Xni（平均）が、nが無限大となる極限において確率 1 で、1／6 に収束するというのが大数の強法則となります。

 

じゃあ、大数の法則と中心極限定理の関係は？

次に、大数の法則と中心極限定理の関係をみていきましょう。

大数の弱法則とは、標本平均はnを十分大きくすると、分布の平均から大きくはずれないというもの。

それに対して、中心極限定理とは、標本平均―分布の平均の挙動が、どれくらいのスピードでどのように0に近づくかを深堀したものと言えます。

その意味で、中心極限定理は大数の弱法則とほぼ同義であると言えますし、大数の法則を精密化したものとも言えるのです。

 

中心極限定理の具体例

では、中心極限定理の具体例を見ていきましょう。

中心極限定理は、広い範囲で使われています。

 

中心極限定理の例1

街でランダムに人の体重を聞き、その分布をとると人のサンプル数が多ければ、多いほどその分布が正規分布に近づく。

中心極限定理の例2

選挙の後、全体の投票結果は開票しないと分からない。

しかし、出口調査などで入手したランダムサンプリングデータは、中心極限定理によると平均は母集団の平均を中心とした正規分布に従い、その分散はサンプル数が大きくなると小さくなるので、全体の開票結果がなくても、おおよその投票結果が推測ができる。

中心極限定理の例3

空気中にたばこの煙を細い穴から放出するとする。

たばこの煙の粒子は空気分子にぶつかってランダムに移動するが、その穴を中心とした断面をとると、中心極限定理により煙が正規分布の形に噴き出していることがわかる。

中心極限定理についてまとめ

いかがでしょうか。

中心極限定理の理解が深まったでしょうか。

中心極限定理は大数の弱法則を精密化したものと言えますし、中心極限定理の持つどんな分布をする集団でも強引に正規分布にしてしまえるという性質は、統計学において極めて重要なのです。

本記事をきっかけに、ここでは取り扱わなかった中心極限定理の証明にもチャレンジしてさらに理解を深めてくださいね。