この記事では「Win Ratioを使った統計解析とは？95%信頼区間や検定手法も解説」としてお伝えいたします。
- Win Ratio（Win比）はどんな解析手法？
- Win Ratio（Win比）のコンセプトは
- Win Ratioの95%信頼区間と検定方法は？
といったことをわかりやすく解説します！
Contents
Win Ratio（Win比）はどんな解析手法？
まずはWin Ratioを使った解析手法とはそもそもどんな手法で、どんな目的で使われているのかを整理しましょう。
結論から言えば、Win Ratioを使った解析手法は、複合エンドポイント（Composite Endpoint）に対する解析手法です。
原著論文としては、おそらくこちら。
複合エンドポイントに対する従来の解析
複合エンドポイントに対する従来の解析としては、「いずれかのイベントのうち、最も早くイベントが発生したら、その時点をイベント発生とする」という定義で解析されます。
例えば、「CVイベントによる死亡」と「心不全による入院」の2つを複合エンドポイントとした時に、「2つのうちどれか一番早いイベントが起こったらイベントありとする」という定義にするということ。
そして、複合イベント発生までの「時間」を解析したい場合には、生存時間解析の枠組みで解析されます。
つまり、ログランク検定、カプランマイヤー曲線、Cox比例ハザードモデル、などで解析するということですね。
もしくは、ある時点（2年、5年など）までの複合イベント「発生の有無」を解析したいとなれば、2値のカテゴリカルデータの解析を実施します。
つまり、カイ二乗検定、フィッシャーの正確確率検定、ロジスティック回帰、などで解析するということです。
複合エンドポイントに対する従来の解析の問題点
従来の解析だと一つ問題点があります。
それは、複合したイベントは全て「臨床的に同じ意味である」として解析する点です。
しかし、入院より死亡の方が臨床的には重いイベントなはず、という印象はありますよね。
そのため、死亡の方を優先順位高く解析したい。
でも死亡だけをエンドポイントにするとイベント数としては少なくなってしまい、検出力が不足してしまう。
だからこそ、複合エンドポイントを使うことは変えたくないが、イベントに優先順位をつけたい、という目的で提案されているのがWin Ratioの解析なんです。
Win Ratio（Win比）のコンセプトと検定方法
Win Ratioが「複合エンドポイントを使うことは変えたくないが、イベントに優先順位をつけたい」という目的で使われることがわかりました。
では実際にどんな手順なのかを詳しく解説していきますね。
想定としては
- 新規治療群と標準治療群の2群比較
- 複合エンドポイントは「CVイベントによる死亡」と「心不全による入院」とする
- そして、「CVイベントによる死亡」の方が優先順位が高い
ということを想定します。
原著論文で提案されていたのは2通り。
- matched pair approach
- unmatched approach
それぞれ見ていきましょう。
matched pair approachとは？
matched pair approachでは、以下の4つの手順で実施されます。
- 背景情報のリスク因子などの情報に応じて標準治療群と新規治療群の患者をマッチングさせる
- マッチングした症例に対して以下に示す5つの分類をする
- 5つの分類の数を数えて勝利数と敗戦数を算出
- Win Ratioの計算
まず、背景情報のリスク因子などの情報に応じて標準治療群と新規治療群の患者をマッチングさせます。
マッチングした数が試合数、ということになります。
マッチングする際に、背景情報があまりに異なる被験者同士でWin Ratioの解析をすると「有利/不利」が出てしまうので、リスク因子を考慮しながらマッチングします。
イメージとしては傾向スコアマッチングのような感じですね。（あくまでイメージです）
そして、マッチングした症例に対して次の5つの分類をします。
- 新規治療群で「CVイベントによる死亡」が早く発生：新規治療群がLose…(a)
- 標準治療群で「CVイベントによる死亡」が早く発生：新規治療群がWin…(b)
- 新規治療群で「心不全による入院」が早く発生：新規治療群がLose…(c)
- 標準治療群で「心不全による入院」が早く発生：新規治療群がWin…(d)
- 上記のうちどれでもない：引き分け…(e)
ここでの注意は「CVイベントによる死亡」の方が優先順位が高い、という想定なので、(a)か(b)の決着がついたら、(c)以下の判定は行わない、ということです。
そして、全てのマッチングに対して上記の5つの分類ができたら、5つの分類の数を数えて勝利数と敗戦数を算出します。
それぞれNa, Nb, Nc, Nd, Neとするとき、
- Na+Nc=NL：敗戦数
- Nb+Nd=NW：勝利数
という定義で敗戦数と勝利数を計算します。
ここまで計算できたら、あとはWin Ratioを算出すればいいだけ。
Win Ratio：RW=NW/NL
つまり、敗戦数に対する勝利数の比を示している、ということです。
unmatched approachとは？
次に、unmatched approachを解説します。
基本的にはmatched pair approachと同じで、最初の手順だけ異なります。
- 各群の症例数の総当たりを試合数にする
- 上記の試合数分だけ、以下に示す5つの分類をする
- 5つの分類の数を数えて勝利数と敗戦数を算出
- Win Ratioの計算
unmatched approachなので、マッチングということは行いません。
ではどうやって試合数を決めるかというと、各群の症例数の総当たりを試合数にします。
例えば新規治療群500人、標準治療群500人の場合、500*500=250,000が試合数になるのです。
試合数が決まれば、それ以降の手順はmatched pair approachと同じなので割愛しますね。
Win Ratioに対する95%信頼区間と検定手法
Win Ratioの算出方法がわかったところで、最後に95%信頼区間と検定手法をお伝えします。
95%信頼区間は、次の2つの手順です。
- 勝利割合とその95%信頼区間を計算
- Win Ratioの95％信頼区間を計算
まずは、勝利割合を計算します。
勝利割合（pw）は次の通りです。
pw=NW/(NW+NL)
そして、二項分布の分散の計算を基にして、95%信頼区間を計算します。
原著論文を引用させていただくと、以下の通り。
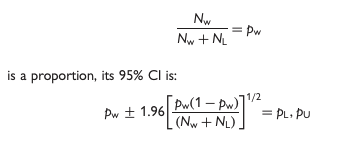
勝利割合の95%信頼区間が計算できたら、Win Ratioの95%信頼区間を計算します。
pL/(1-pL)が信頼区間の下限になり、pU/(1-pU)が信頼区間の上限になります。
そして、検定手法としてはZ検定を用います。
Z検定自体はとても有名な検定手法なので、ここでは割愛させていただきますね。
Win Ratio（Win比）を使った論文紹介
Win Ratioは、最近徐々に使われている印象です。
例えば、こちらの論文。
2022年にパブリッシュされていますが、Fig2を見ると4つの複合エンドポイントに対してWin Ratioを計算していることがわかりますね。
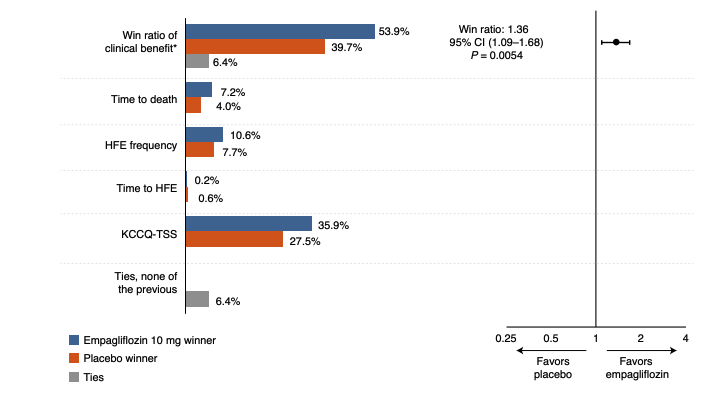
まとめ
いかがでしたか？
この記事では「Win Ratioを使った統計解析とは？95%信頼区間や検定手法も解説」としてお伝えいたしました。
- Win Ratio（Win比）はどんな解析手法？
- Win Ratio（Win比）のコンセプトは
- Win Ratioの95%信頼区間と検定方法は？
といったことが理解できたのなら幸いです！
こちらの記事の内容は動画でも解説しておりますので、併せてご確認くださいませ。
第1章：臨床研究ではなぜ統計が必要なのか？計画することの重要性
第2章：研究目的をどれだけ明確にできるのかが重要
第3章：p値で結果が左右される時代は終わりました
第4章：多くの人が統計を苦手にする理由
第5章：統計を使えるようになるために今日から何をすれば良いか？
第6章：統計を学ぶために重要な環境
もしあなたがこれまでに、何とか統計をマスターしようと散々苦労し、何冊もの統計の本を読み、セミナーに参加してみたのに、それでも統計が苦手なら…
私からプレゼントする内容は、あなたがずっと待ちわびていたものです。
