この記事では「統計学で頑健性がある(ロバストである)」ということの意味について考えていきます。
- 統計学における「頑健性」の意味は?
- 多変量解析などのモデル解析での頑健性
- 頑健性を担保するには?
ということが理解できるようになりますよ!
統計学における「頑健性(ロバスト)」の意味をわかりやすく解説!

まずは統計における「頑健性」の意味を考えていきましょう。
実は統計解析には「仮定」が含まれていることがほとんどです。
例えば、最も有名な統計的検定であるT検定は「データが正規分布である」という仮定を持って解析しています。
しかしながら、実際のデータは必ずしも正規分布に当てはまったデータが出てくるとは限らないですよね。
なので、「仮定」を外した時にも同じ結論が得られるかどうかが重要になってくるんです。
具体的に言えば、T検定で実施した結論と同じ結論が、ノンパラメトリック検定であるマンホイットニーのU検定でも得られるのか?という観点が重要。
ここで言うところの「同じ結論」とは、「どちらの解析でも有意/有意じゃない」が同じになる、ということです。
パラメトリック検定とノンパラメトリック検定では解析手法が異なるので、得られる結果(P値)は異なりますが、それでも同じ結論(有意/有意じゃない)が得られるのであればその結果には頑健性があることになります。
重要なことは「仮定」が正しいか正しくないか、という正解/不正解が重要ではない、ということ。
仮定が正しくても、仮定が正しくなくても、同じ結論が得られることが最も重要だ、という視点です。
多変量解析などのモデル解析での頑健性

この「頑健性」の考え方は、統計学的検定だけに限りません。
多変量解析などのモデル解析でも頑健性の考え方は重要です。
なぜなら、多変量解析などのモデル解析でも多くの仮定が含まれていることがあるからです。
例えば、「残差が正規分布している」とか「多変量解析に含んでいる説明変数の数や種類が最適である」といった前提(仮定)があります。
こういった仮定をずらした時にも同じ結論を得られるのか?という、頑健性を考えることが重要。
欠測値のあるデータの取り扱いにはかなり強い仮定があることも
また、欠測値のあるデータを扱う時にも、かなりの仮定を含みます。
例えば、LOCF(Last Observation Carried Forward)という単一補完の方法の一つを考えてみます。
LOCF(Last Observation Carried Forward)は、最後に得られたデータで欠測値を補完する方法。
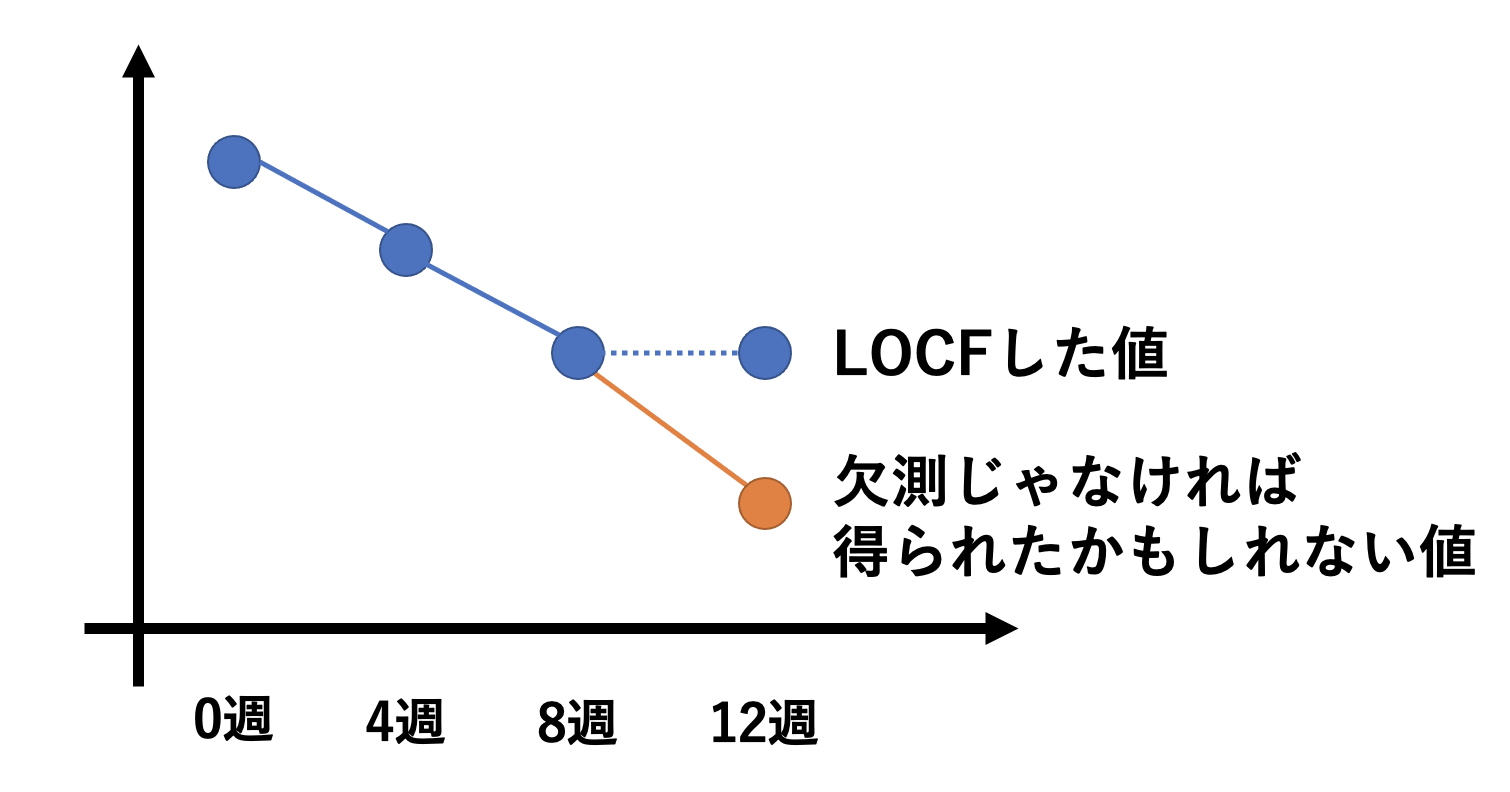
上記のように、12週のデータが欠測だった場合、直前の8週のデータを12週のデータとして補完します。
しかし、欠測じゃなければもしかしたらオレンジの点のようなデータになっていたかもしれません。
このように、LOCFには「最後に得られたデータがずっと続く」という強い仮定があるんです。
だから、欠測値の考え方を変えた解析手法でも実施し、同じ結論を得られるのかという頑健性を確認することが重要です。
頑健性を担保するには?

じゃあ頑健性を担保するにはどうしたらいいのでしょうか?
方法としては、複数の解析を実施しても同じ結論が得られるかどうかを確認する、ということ。
医学研究では「感度解析(Sensitivity analysis)」が使われています。
感度解析の例としては、
- 多変量解析に含めている説明変数を変える
- 欠測値の考慮方法を変える
- 解析対象集団を変える
といったことが考えられますね。
例えばこちらの論文だと、以下のような記載がありました。
.jpg)
多変量解析として「年齢」を含めた解析をメインとしているのですが、感度解析(Sensitivit Analysis)として「年齢」を除外した際に同じような結論(Similar findings)が得られるかどうかを実施しています。
このように、仮定を変えた複数の解析を実施し、同じ結論を得られるのであれば頑健性があると言うことができます。
まとめ

いかがでしたか?
この記事では「頑健性がある(ロバストである)」ということの意味について考えました。
- 統計における「頑健性」の意味は?
- 多変量解析などのモデル解析での頑健性
- 頑健性を担保するには?
ということが理解できるようになったのなら幸いです!
こちらの内容は動画でも解説していますので、併せてご確認くださいませ。













コメント