この記事は「JMPで層別解析のコクランマンテルヘンツェル検定を実施する方法!」ということでお伝えします。
コクランマンテルヘンツェル検定(Cochran-Mantel-Haenszel検定)とは層別解析の一つ。
コクランマンテルヘンツェル検定(CMH検定)は「2×2分割表で使われる検定」であり「層別因子を考慮することができる検定」である解析手法です。
統計解析ソフトのJMPでもコクランマンテルヘンツェル検定(CMH検定)が実施できますので、その方法をお伝えしますね!
コクランマンテルヘンツェル検定の前に層別解析についてちょっとだけ復習

コクランマンテルヘンツェル検定(CMH検定)の実施方法をお伝えする前に、層別解析ってそもそも何だったっけ?という事で、ちょっとだけ復習しましょう。
層別因子についての詳細は「層別解析とサブグループ解析の違いは?統合方法や結果の見方もわかりやすく!」の記事をご参照ください。
層別因子はICH E9に定義の記載があります。
つまりここから分かるのが
- 層別因子は割付(ランダム化)の際に考慮すべき因子のこと
- 層別因子は疾患の予後に影響があると考えられる因子のこと
ということですね。
層別因子を考慮したランダム化である「層別ランダム化」というのがあります。
層別ランダム化とは、例えば、性別(男性と女性)が疾患の予後に影響がありそうなので層別因子として考えたい、とします。
この時に、被験者が男性か女性かに応じて、男性ごとにランダム化・女性ごとにランダム化、という作業をするのです。

層別因子のカテゴリごとにランダム化することによって、プラセボ群で実薬群で、男性と女性のバランスが取れることが期待できるのです。
そして、層別因子を考慮したランダム化を実施した後は、解析段階でもその層別因子を考慮することが推奨されています。
「層別因子を考慮した解析」の一つが層別解析ですね。
そして、層別解析の一つがコクランマンテルヘンツェル検定(CMH検定)なのです。
JMPで層別解析のCochran-Mantel-Haenszel検定を実施!

では実際に、統計解析ソフトのJMPでコクランマンテルヘンツェル検定(CMH検定)を実施していきましょう。
サンプルデータを使っていきますので、JMPユーザーであれば誰でも再現可能です。
JMPでコクランマンテルヘンツェル検定を実施するデータ
使うデータとしては、サンプルデータのConsumer Preferenceです。
「カテゴリカルなモデル」の中にあるサンプルデータですね。

想定するQuestionは以下の通りです。
では実際にやっていきましょう!
JMPでコクランマンテルヘンツェル検定を実施する前に交絡バイアスを確認!
まずは単純に子供の有無ごとに趣味の有無が関連しているかを確認していきましょう。
つまり、子供の有無ごとに趣味の有無が関連しているか、という事に関してカイ二乗検定を実施していきます。
JMPでは「分析 > 二変量の関係」を選択します。
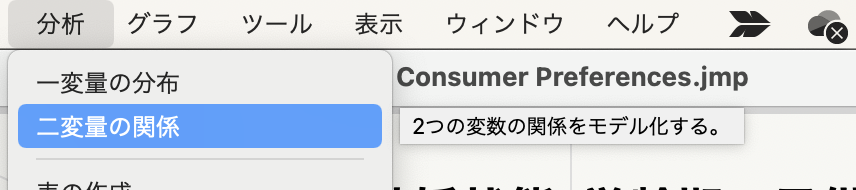
Xに学齢期の子供、Yに仕事以外にいろいろな趣味がある、を選択します。
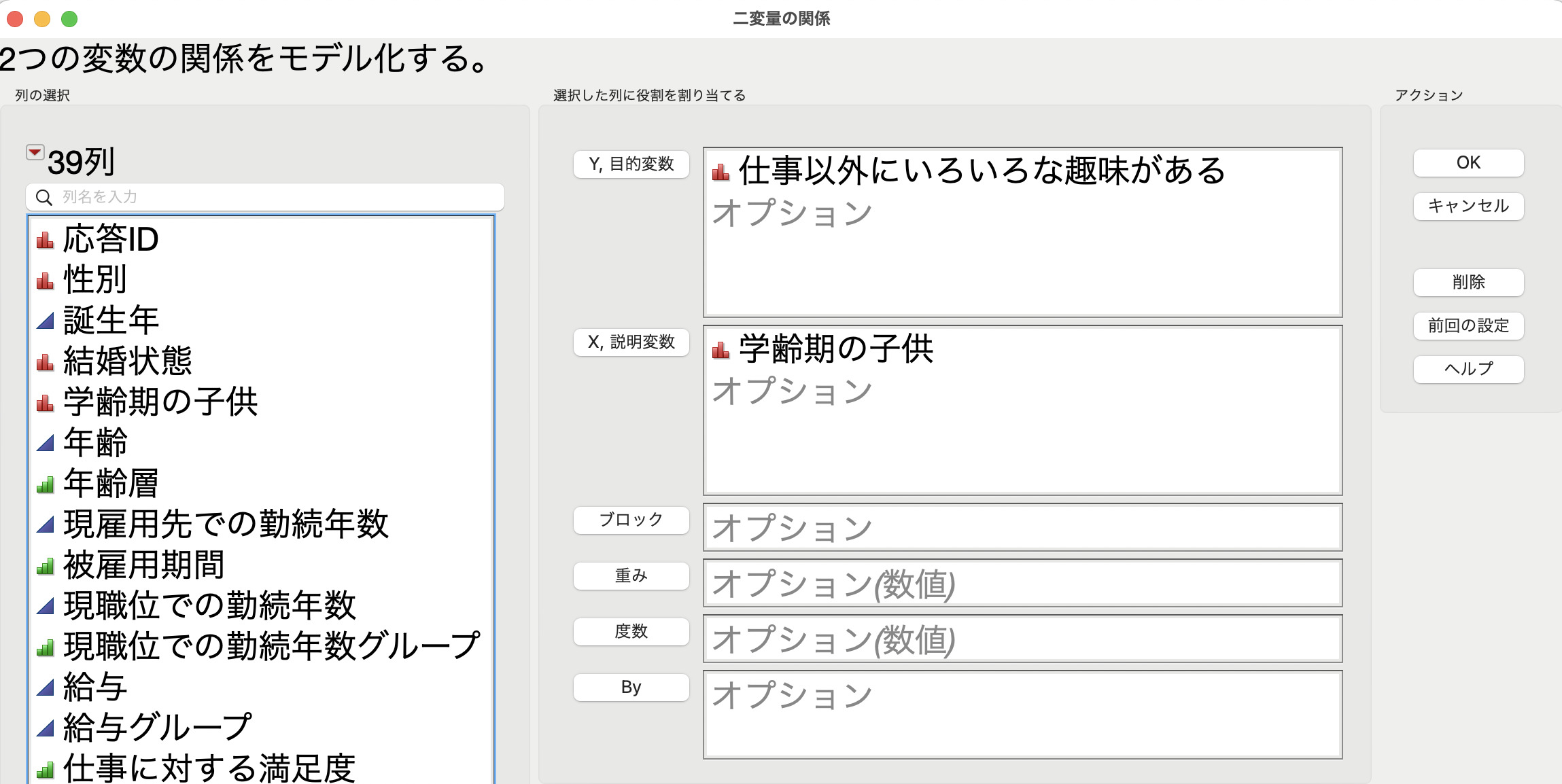
そうすると下記の結果が得られ、子供の有無ごとに趣味の有無が関連していそうだという結果が得られました。

では次に、性別が交絡していないか?を確認していきます。
交絡バイアスを引き起こす交絡因子の条件としては、
- アウトカムに関連がある
- 説明変数側とも関連がある
ということなので、「性別と趣味の有無の関連」「性別と子供の有無の関連」の2つをみていきます。
まずは、「性別と趣味の有無の関連」です。
同様にカイ二乗検定をやってみると、関連がありそうかもしれない、という結果が出ています。

では次に、「性別と子供の有無の関連」です。
同様にカイ二乗検定をやってみると、関連がありそうかもしれない、という結果が出ています。
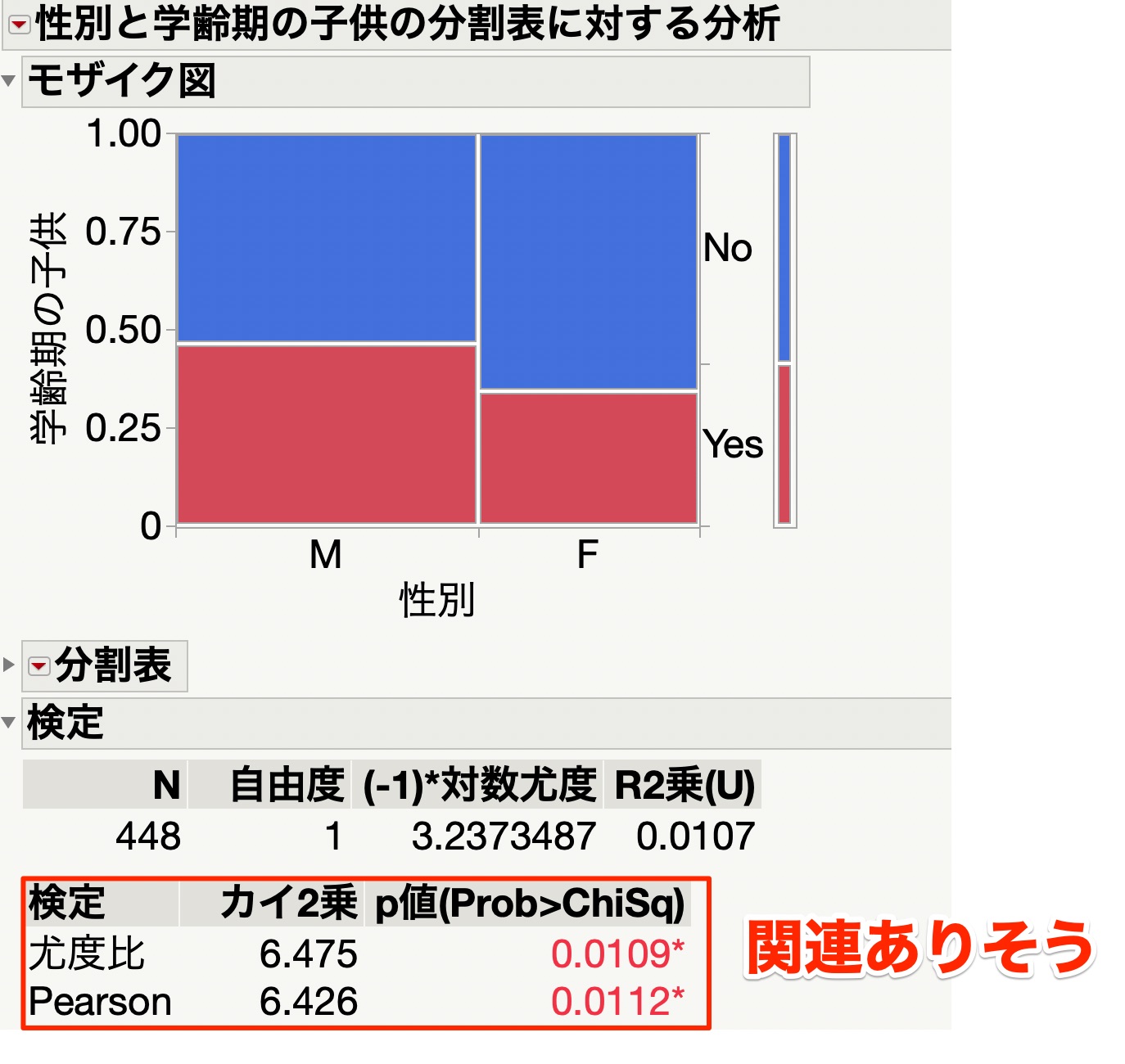
つまり今回のデータでは、性別は
- アウトカムに関連がある
- 説明変数側とも関連がある
という条件を満たしていそうなので、性別を考慮した解析を実施しよう、という事になります。
JMPでコクランマンテルヘンツェル検定を実施!
では、性別を考慮した層別解析である、コクランマンテルヘンツェル検定をJMPで実施していきます。
まずはカイ二乗検定を実施するでOKなので、子供の有無ごとに趣味の有無が関連しているか、という事に関してカイ二乗検定を実施していきます。
JMPでは「分析 > 二変量の関係」を選択します。

Xに学齢期の子供、Yに仕事以外にいろいろな趣味がある、を選択します。

そうすると下記の結果が得られ、子供の有無ごとに趣味の有無が関連していそうだという結果が得られました。

ここからがCMH検定をする方法です。
赤い三角形からCochran-Mantel-Haenszel検定を選択します。

性別を選択します。
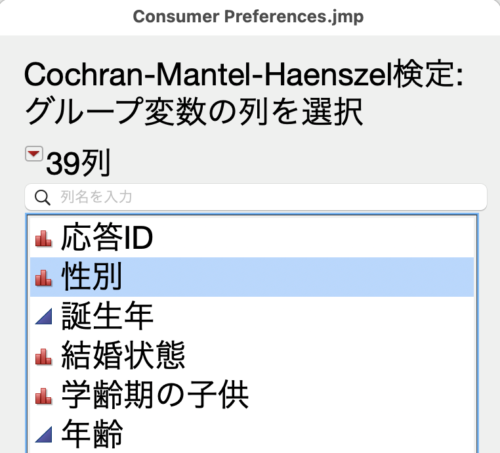
すると下記の結果が得られ、層別因子(性別)を考慮したとしても関連がありそうだという結果になりました。

まとめ

いかがでしたか?
この記事は「JMPで層別解析のコクランマンテルヘンツェル検定を実施する方法!」ということでお伝えしました。
JMPでは通常のカイ二乗検定を実施した後に、赤い三角形からCochran-Mantel-Haenszel検定を選択することで実施できました。
ぜひご自身でもやってみてください!












コメント