共分散分析という解析手法があります。
英語ではAnalysis of Co-Varianceと呼ばれるため、省略してANCOVA(アンコバ)とも呼ばれていますね。
共分散分析は、医薬統計を学ぶ上では必ず理解しておく必要がある解析手法。
論文でも、かなり使われているのを見ます。
実際に、私も医薬統計の解析の50%程度は共分散分析で解析します。
でも、何となくイメージしづらい共分散分析。
「分散分析」が名前に入っているから、検定手法の1つ?
でも「共」ってどういう意味?
このページではそんな疑問を、わかりやすい例を用いて解説していきます。
共分散分析(ANCOVA)とは交絡因子を共変量として考慮できる解析手法

共分散分析が何をやっている手法か、結論から先に言います。
共分散分析は、平均値に影響を及ぼすデータ(共変量)があった時に、その共変量の影響を取り除いて群間を比較することができる、解析手法
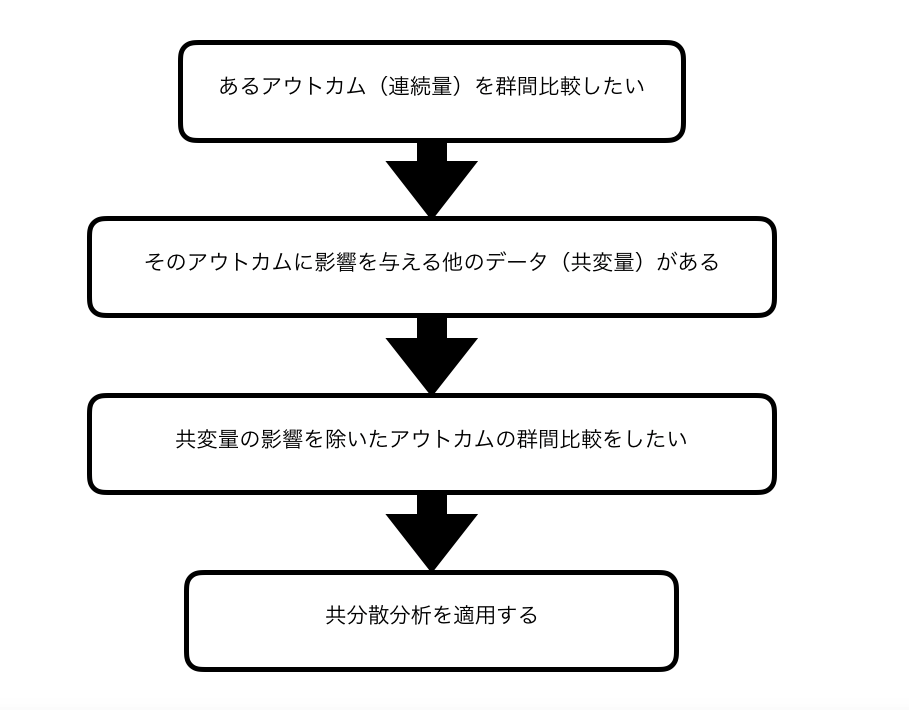
他の言い方をすると、「分散分析」に「回帰分析」を応用したもの。
つまり、特徴としては「分散分析」の特徴と、「回帰分析」の特徴を持ち合わせています。
そのため、基本的に共分散分析は分散分析と同じように「群間比較」を目的として使われる統計手法です。
分散分析という言葉からもわかる通り、比較する群の数は3以上でも大丈夫です。
そして回帰分析のように、関係を式で表すことができ、説明変数と目的変数の関係がわかるようになっています。
共分散分析(ANCOVA)はどこで使う?交絡バイアスを思い出しましょう。
注意すべきバイアスは、3種類ありました。
「選択バイアス」「情報バイアス」「交絡バイアス」ですね。
そのうち交絡バイアスとは、交絡因子により結果が歪められてしまうバイアスのことでした。
平均値に影響を及ぼすデータ(共変量)が群間で異なっていれば、それがいわゆる交絡因子になります。
つまり、共分散分析を用いることにより交絡因子の影響を調整することができます。
言い換えると、共分散分析で交絡因子の影響を小さくすることが可能です。
もはや、魔法のような解析手法です!
私が初めて共分散分析を理解した時、本当に魔法かと思い、立ち尽くしてしまいました。
なぜかというと、一般的にバイアスを排除できるかどうかは、試験の計画段階(データを集める前)に決まってしまいます。
解析段階(データを集めた後)にバイアスを排除することは、かなり難しい。
ですが、この交絡バイアスだけは、共分散分析を使うことにより、(完全ではないが)ある程度排除ずることが可能なのです。
交絡因子と共変量の違いは?
ここで、ちょっとだけ用語の整理を。
「交絡因子」と「共変量」の違いですね。
上記でみたように、交絡因子とは交絡バイアスを引き起こす因子のこと。
そして共変量とは共分散分析で調整する説明変数のこと。
特に連続変数である説明変数のことを共変量と呼びます。
そのため、交絡因子を共分散分析で調整するのであれば、その因子は交絡因子であり、かつ、共変量です。
ですが、交絡因子であっても共分散分析で調整しないのであれば、共変量ではない、ということになります。
共分散分析(ANCOVA)を例を使ってわかりやすく

共分散分析は分散分析に回帰分析を応用した手法なので、式で書くことができます。
具体例で考えたほうがわかりやすいため、以下の例を考えてみます。
例)A社とB社の年収を比較する
A社の平均年収:500万円
B社の平均年収:550万円
これを見た時に「あ、B社の方が平均年収高い」と素直に思えますか?
同じ業務内容だったら、B社に行きたいですか?
実は、もうちょっと詳細な情報がないとB社に行きたいとは思わない方がいいですよね。
共分散分析(ANCOVA)の例:年収に影響の与える因子はあるか?
私が平均年収の情報を見る際に、必ず気にすることがあります。
それは「その会社の平均年齢はいくつだろう?」ということ。
なぜなら、一般的に年齢が高くなれば、年収も上がっていく傾向があるためです。
つまり、平均年収が高い要因として、2つの可能性があります。
- 本当にその会社の給与水準が高い
- その会社の従業員の年齢が高い
もしB社の平均年収が高い要員が、1の「本当にその会社の給与水準が高い」であれば、B社に行きたいですよね。
ですが、B社の平均年収が高い要員が、2の「その会社の従業員の年齢が高い」であれば、ちょっと考えたくないですか?
つまり言い換えるとこういうことです。
A社とB社の平均年収の差は、本当にA社とB社の会社の違い(給与水準の違い)によるものなのか、その会社の従業員の年齢の違い(年齢という交絡因子の違い)によるものなのかを明らかにしないと、真実がわからない
なので、「本当にA社とB社の給与水準の違い」なのか「年齢という交絡因子」によるものなのかを解析してみよう!ということになります。
共分散分析で、どちらの影響なのかを解析する
そこで登場するのが、共分散分析です。
共分散分析の特徴である「結果に影響を与える他のデータの影響を調整することができる」を今回の平均年収の例で言い換えてみます。
「年収に影響を与えていると考えられる、年齢の影響を調整することができる」
さらに言い換えると、こうなります。
「年収に影響を与えていると考えられる、年齢の影響を除いたA社とB社の比較ができる」
これってすごいと思いませんか?
本当に魔法のような解析手法だと、改めて思います。
そして、肝心の式です。
a1, a2はそれぞれ係数と呼ばれています。
bは切片と呼ばれています。
共分散分析(ANCOVA)は重回帰分析と何が違うの?
この式はどこかで見たことありませんか?
年収 = a1*会社 + a2*年齢 + b + 誤差
これって、回帰分析の章で示した以下の式と形が一緒ではないでしょうか?
Y(体重)=a*x1(身長)+c*x2(年齢)+b+誤差
そう、実は重回帰分析と共分散分析は、同じような式で示すことができます。
では何が違うか。
それは、共分散分析の「分散分析」という部分に隠されています。
分散分析とは、3群以上の群の平均値を比較する検定手法でした。
つまり、共分散分析では、群間比較の部分が入っている、ということになります。
群間比較を目的とする多変量解析なのであれば群という説明変数が最も重要であり、それ以外の説明変数は交絡バイアスを低減するために含めています。
そのため、説明変数の重要度に優劣がある場合、共分散分析と呼んでいます。
今回の例でいうと、「会社」というのはA社かB社の2つの名義尺度の群を示す説明変数ですよね。
なので、この共分散分析の結果から、A社とB社の群比較の結果が出てきます。
一方で重回帰分析はというと、最も重要な説明変数が特になく、全ての説明変数が並列な重要度を持っている場合のことを指しています。
共分散分析を、実際の数値例で理解する
ではA社とB社の年収と年齢に関して、実際に解析してみます。
下記の表の通りの設定で乱数を発生し、共分散分析を実施してみます。
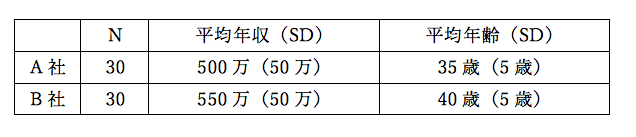
そして乱数発生の結果、以下のような結果が得られました。

共分散分析(ANCOVA)の例:まずは単純にT検定してみる
この平均年収を、まずは単純にT検定してみます。
すると、T検定の結果は以下のように得られました。
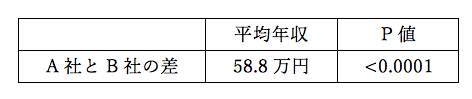
単純にA社とB社の平均年収を比較しただけですので、その差は58.8万円です。
そしてP値はかなり小さく、0.0001未満という結果が得られました。
では共分散分析で年齢を調整するとどうなるか?
では次に、年齢を共変量とした共分散分析を実施してみます。
すると、以下のような結果が得られました。

それでは、単純なT検定と、年齢で調整した共分散分析の結果を並べてみます。

驚くべきことに、年齢で調整すると平均年収の差が小さくなっているとともに、そのP値も大きくなっています。
もし0.05を有意水準にして検定を実施していた場合には、有意差があったものが有意差なしになるという、大きな結論の違いにつながります。
共分散分析(ANCOVA)とT検定ではなぜ結果の違いが出てくるの?

なぜこのような結果の違いにつながったのでしょうか。
ここからは、散布図を元にイメージを深めていきましょう。
年齢と年収の散布図を描くと、以下のようなイメージになります。
(実際のデータではありません。イメージがつきやすいように、かなり誇張して極端な散布図にしています。)
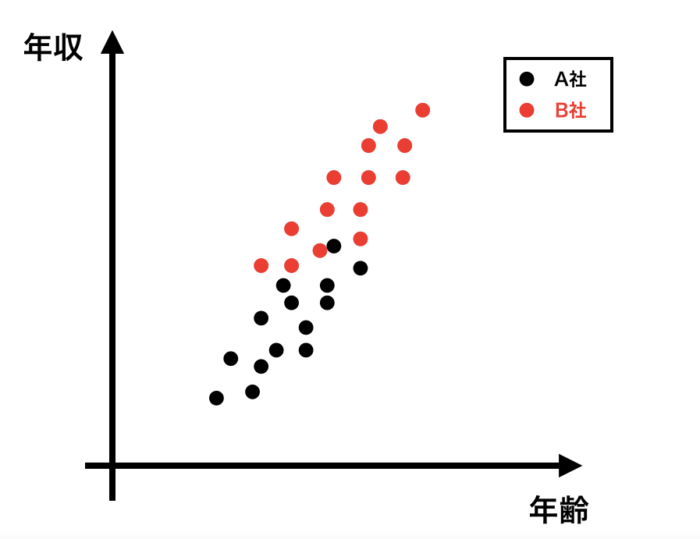
T検定はA社とB社の平均年収を単純に比較したものです。
単純な比較なので、X軸の年齢は全く考慮していません。
つまりY軸の単純な比較になります。

では共分散分析では何をやっているのか。
共変量で調整する(今回の場合は、年齢で調整する)というのは、下記のようにそれぞれの群で平行な直線を引く、ということに相当します。
そしてその2つの直線の差が、共分散分析で出てくるA社とB社の差、ということになります。
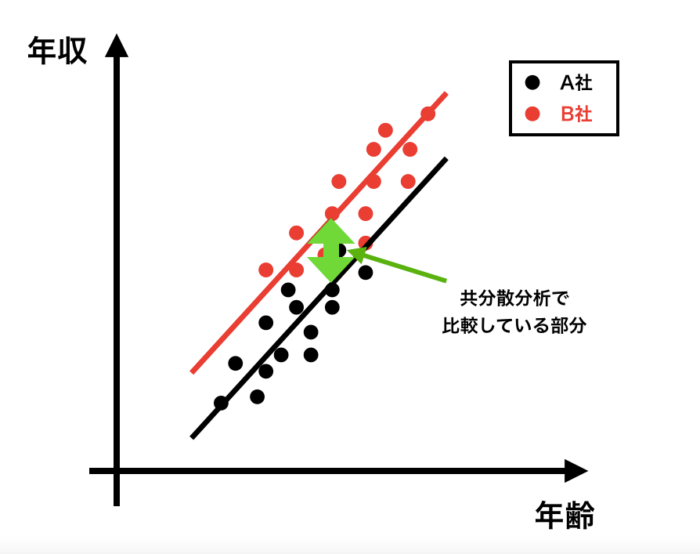
直線の差を比較しているため、「仮に同じ共変量の値だった時(同じ年齢だった時)のY(年収)の差」を比較していることと同じことを意味します。
共分散分析(ANCOVA)で交絡バイアスを除くことができるという利点
共分散分析がとても有用な理由は、「交絡バイアスを除くことができる」という点です。
バイアスのほとんどは、試験の計画時に考慮し、排除するような計画を立てる必要があります。
しかしながら、交絡バイアスだけはデータを取得した後に、解析で排除することが可能なのです。
医薬統計を学ぶ上で、交絡バイアスは、絶対に理解しておいてください。
例を用いて、自分で身近な交絡バイアスを考えてみるのも良いです。
共分散分析(ANCOVA)に関するまとめ

- 共分散分析は、平均値に影響を及ぼすデータ(共変量)があったとき、その共変量の影響を取り除いて群間比較をするための解析手法。
- 共変量と解析結果の直線の差を比較している。
動画でも共分散分析を解説していますので、この記事と併せて確認いただけると理解が深まるはずです。
統計に関するご質問があれば、メルマガにご登録の上ご質問くださいませ!














コメント
コメント一覧 (8件)
[…] 共分散分析はどんな解析手法?散布図を使って分かりやすく解説! […]
[…] 共分散分析はどんな解析手法?散布図を使って分かりやすく解説! […]
[…] そして、回帰分析を理解することは、共分散分析を理解することにつながります。 […]
[…] >>共分散分析にかんして深く理解する! […]
[…] >>>共分散分析とは?論文でも使われるANCOVAをわかりやすい例で! […]
[…] 共分散分析やロジスティック回帰分析、Cox比例ハザードモデルの解釈にも重要な知識ですので、是非マスターしましょう! […]
[…] 重回帰分析(目的変数が連続変数の場合:共分散分析) →n数を15で割った数まで […]
[…] これ以降は、マッチング後のデータを使って共分散分析やCox比例ハザードモデルなどの多変量解析を実施することが多いかな、という印象です。 […]