交絡因子とは？中間因子など統計的な意味を事例でわかりやすく簡単に

交絡因子は医学統計において、かなり重要な知識であるにも関わらず、とてもイメージしにくいです。

「交絡」「交絡因子」「交絡バイアス」など、交絡に関する用語が結構出てくるため、色々と混乱が生じやすいですね。

そのためこのページでは、交絡バイアスを引き起こす交絡因子の意味や用語の定義を整理して解説し、豊富な例で交絡因子を理解していきます。

3種類あるバイアスの中で一番わかりにくいけど、でも一番重要な交絡因子。

ぜひ理解してくださいね。

 

交絡因子とは？バイアスを引き起こす３条件

交絡バイアスを発生させる因子のことを、交絡因子と呼びます。

日本疫学会によると、ある因子が交絡因子となるためには、以下の３つが成立していることが条件です。

 

 

言葉だけではわかりにくいので、交絡因子の条件を図式化すると以下の通りです。

 

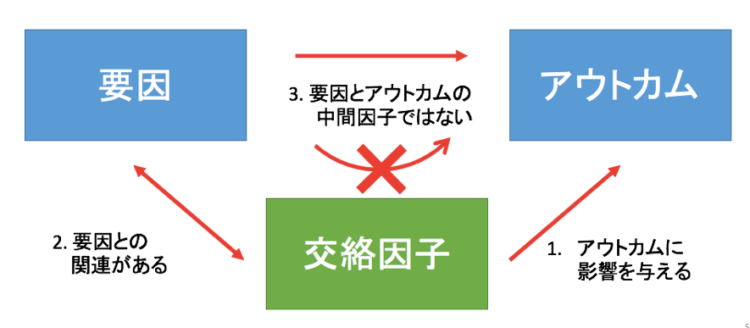
上記の３つが揃って入れば、その因子は交絡因子ということになります。

交絡因子の説明としては以上ですが、それだけではわかりにくいと思うので、例を用いて説明します。

 

交絡の例１：高血圧ほど高収入になるか？

 

ある一つの事実があります。

「高血圧であれば高収入である」

ということです。

 

え・・・・。

 

と思いますよね。

この「高血圧であれば高収入である」ということをどのように捉えれば良いでしょうか？

これを聞いた奥様方は、今晩の夕食から塩辛い味付けにすれば、旦那さんは高収入になるのでしょうか？

でもそんなことしたら、高収入になる前に病気になりそうですね。。

 

みなさんも何となくお気づきかもしれませんが、この「高血圧であれば高収入である」という事実に関して、何らかの交絡因子の影響があります。

あなたはどんな因子を思い浮かべますか？

 

実は、「年齢」という交絡因子があることで、「高血圧であれば高収入である」という事実が生じるのです。

では、この「年齢」が本当に交絡因子なのか、交絡因子の3つの条件に当てはめてみましょう。

 

交絡因子の条件1： アウトカムに影響を与えているか？

交絡因子の１つ目の条件を確認しましょう。

１つ目の条件は「アウトカムに影響を与えている」でした。

この「高血圧であれば高収入である」の例でアウトカムとは何でしょうか？

「高収入である」ということですね。

 

では問題です。

 

あなたはどう思いますか？

やっぱり年齢は収入に影響を与えていますよね。

一般的には歳をとるにつれて様々な経験をし、スキルも持ち合わせているので、高収入になっていきます。

また、残念なことに日本ではまだ年功序列の文化が少なからず残っています。

この「年齢が高くなれば高収入になる」というのは言えると思います。

 

交絡因子の条件2： 要因との関連があるか？

交絡因子の２つ目の条件を確認しましょう。

２つ目の条件は「要因との関連がある」でした。

この「高血圧であれば高収入である」の例で要因とは何でしょうか？

「高血圧」ですね。

この例でいうところの要因とは「高血圧」ということです。

 

ではまたまた問題です。

 

ありそうですよね。

以下の表は年齢別の平均血圧を示しています。

表を見ていただきたくと分かりますが、年齢が上がるにつれて平均血圧も高いですね。

そのため、条件の二つ目である「要因との関連がある」についても、条件を満たしています。

 

平均血圧	20代	30代	40代	50代	60代	70代
男性	120 74	122 78	126 83	135 87	138 84	142 80
女性	108 67	112 71	119 76	127 80	137 82	140 78

 

交絡因子の条件3： 要因とアウトカムの中間因子ではないか？

最後に、交絡因子の３つ目の条件を確認しましょう。

３つ目の条件は「要因とアウトカムの中間因子でない」でした。

この条件が一番イメージしにくいと思います。

 

そのため、まずは「要因とアウトカムの中間因子である」場合に、どういうことが言えるかを解説します。

中間因子である場合には「高血圧の結果、年齢が高くなり、その結果高収入になる」ということです。

一般化すると「要因→因子→アウトカム」という一連の流れが成立する場合に、「要因とアウトカムの中間因子である」といえるのです。

 

この例では、年齢は中間因子ではないですよね。

高血圧になればなるほど年齢が高くなり、その結果として年収が上がる。

こんなことは考えられません。

なので、３つ目の条件も達成することになります。

図式化すると、このようになります。

 

 

 

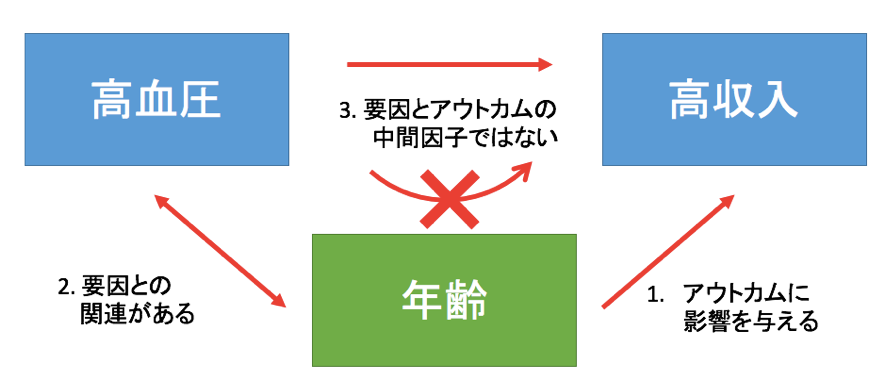
交絡の例２：コーヒーをよく飲む人は心筋梗塞になりやすい？

ある調査によると、このような結果が出たとのことです。

コーヒーをよく飲む人は心筋梗塞になりやすい

これって、本当でしょうか？

もし真実であれば、１日に３杯はコーヒーを飲む私は心筋梗塞まっしぐらということになります。。

 

ですが、これには交絡が絡んでいます。

ということで、「コーヒーをよく飲む人は心筋梗塞になりやすい」に関して、交絡因子を考えます。

 

まず、要因とアウトカムを整理しましょう。

 

喫煙は交絡因子になるか？

「コーヒーをよく飲む人は心筋梗塞になりやすい」が間違っていると仮定します。

すると、違う要因（交絡因子）によって見かけ上、「コーヒーをよく飲む人は心筋梗塞になりやすい」という関係性が出てきただけ、という風に考えることができます。

すると、私たちが考えなければならないことは、以下の２つの条件に当てはまる交絡因子を見つけなければなりません。

 

 

この２つの条件を満たしそうなのは「喫煙」ではないでしょうか。

あなたもぼんやりと「喫煙かもなぁ」ぐらいに思っていたかもしれません。

図式化すると、このような関係があるかもしれないということです。

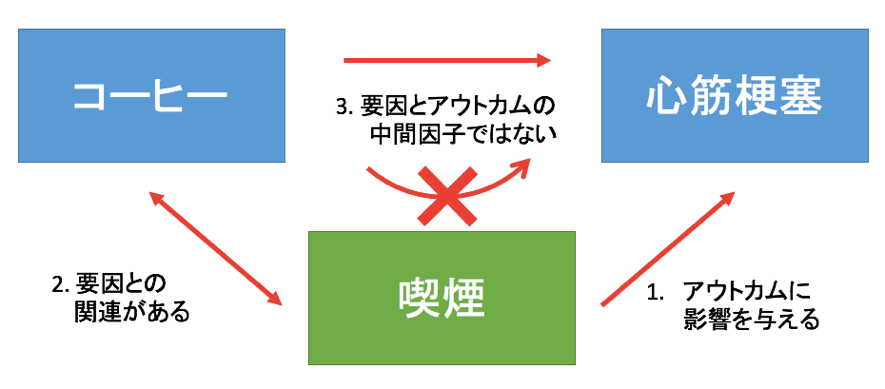
では、この喫煙が交絡因子の３条件に当てはまっているかどうかを考えてみましょう。

 

交絡因子の条件1： アウトカムに影響を与えるか？

まずは、１つ目の条件に当てはまるかどうかを検討してみます。

１つ目の条件とは、「アウトカムに影響を与えるかどうか」でした。

では、今回の「コーヒーをよく飲む人は心筋梗塞になりやすい」に関してのアウトカムはなんだったでしょうか。

 

そう、「心筋梗塞になりやすい」がアウトカムですね。

 

では、喫煙すると心筋梗塞になりやすいか？

と問われれば、それはYesです。

下にも図を貼り付けましたが、

タバコのパッケージにこのような警告がすでにされております。

そのため、１つ目の条件はクリアしております。

 

交絡因子の条件2： 要因と関連があるか？

次に、２つ目の条件に当てはまるかどうかを検討してみます。

２つ目の条件とは、「要因との関連があるかどうか」でした。

では、今回の「コーヒーをよく飲む人は心筋梗塞になりやすい」に関しての要因はなんだったでしょうか。

 

そう、「コーヒーをよく飲む」が要因ですね。

では、コーヒーをよく飲む人は、よく喫煙をするのか。

私自身、正確なデータを把握しておりませんが、これも言えると思います。

喫煙所ではよく缶コーヒーを持っている人を見かけますし、カフェで禁煙席はガラガラなのに喫煙席は満席、といった状況をよく目にするためです。

そのため、二つ目の条件は当てはまりますね。

 

交絡因子の条件3： 中間因子ではないか？

最後に、３つ目の条件に当てはまるかどうかを検討してみます。

３つ目の条件とは、「要因とアウトカムの中間因子ではない」でした。

中間因子という言葉が難しいですが、今回の例ではこういうことです。

「コーヒーをよく飲むことによって、必ずといっていいほどの人が喫煙をする、その結果心筋梗塞になりやすい」

という関係が当てはまるかどうか、ということです。

どうでしょうか？

当てはまると思いますか？

 

当てはまらないですよね。

つまりコーヒーをよく飲む結果として喫煙をするわけではないということです。

私もコーヒーはすごく飲みますが、喫煙は全くしません。

なので、コーヒーを飲むことによって喫煙をする、という関係性は成り立ちません。

よって、中間因子ではないため、３つ目の条件が当てはまっています。

 

最後に、もう一度喫煙が交絡因子であるかどうかの図を提示しておきます。

なんども眺めてみて、喫煙が交絡因子である３つの条件に合致しているか、考えてみてください。

 

交絡因子を排除してバイアスを回避する方法

交絡を排除するためには、デザイン段階で排除する他に統計解析で排除することも可能です。

具体的には、共分散分析という方法です。

共分散分析を使うことで、交絡因子の影響をある程度排除することができます。

また、層別解析も交絡バイアスを排除するための解析手法です。

 

じゃあ解析段階で交絡因子の影響を排除できるからいいじゃないか！

と思うかもしれませんが、あくまで解析段階での排除は、最終手段です。

データの数によっては、交絡因子の影響を排除しきれない場合があります。

そのため、基本的にはバイアスはデザイン段階で排除することが望ましいのです。

 

どういった方法かといえば、ランダム化ですよね。

ランダム化を用いることで既知の因子であろうが未知の因子であろうが、交絡因子を平均的に群間で同じになることが期待できるのです。

 

交絡因子に関するまとめ

交絡バイアスを引き起こす要因を交絡要因と呼びます。

その因子が交絡要因であるかどうかについては、３条件を満たすかどうかで判断します。

 

 

そして交絡因子の排除のためには、解析的には共分散分析などの多変量解析を用いる、ということがアイデアとして挙げられます。

しかし、あくまで解析段階での交絡因子の排除は、最終手段です。

理想はランダム化をすることによって既知の因子であろうが未知の因子であろうが、交絡因子を排除することが重要です！