この記事では、SPSSでシャピロウィルクやKolmogorov-Smirnovなどの正規性の検定を実施する方法について解説します。
例えばT検定を実施する場合。
T検定はデータが正規分布であることを仮定しているパラメトリック検定ですよね。
そのため、事前にデータが正規分布かどうかを検定で判断するケースをよく目にします。
いわゆる、正規性の検定です。
正規性の検定には2種類あって、「Shapiro-Wilkの正規性の検定」と「Kolmogorov-Smirnovの正規性の検定」が有名。
今回の記事では
- そもそも正規性の検定は必要なのか?
- 正規性の検定をSPSSではどうやって実施するのか?
- 「Shapiro-Wilkの正規性の検定」と「Kolmogorov-Smirnovの正規性の検定」の使い分けは?
ということをお伝えしていきます!
そもそも正規性の検定は必要なのか?

単純な疑問として、T検定はデータが正規分布であることを仮定している、と言われても、データが正規分布しているとどうやって判断すればいいのでしょうか?
実際のデータ解析の場で困ってしまう、あるあるのケースですよね。
お察しの通り、「いま手元にあるこのデータは正規分布に従うのだろうか?」という判断は、意外に難しいです!!
尖度(skewness) や歪度(kurtosis)を用いるとか、ヒストグラムを描いて観祭する、という手段が適切だとか、色々な本には書いてますが、なかなか判断がつけられません。
そのため多くの方が、データが正規分布かどうかの判断を「正規性の検定」に委ねてしまっています。
正規性の検定はどんなデメリットがある?
しかし統計専門家からすると、正規性の検定は実施しない方が良いと考えます。
理由は主に二つ。
- 多重性の問題
- サンプルサイズで検定結果は左右される
まずは、多重性の問題。
正規性を判断するときに検定を用いるということは、それだけ検定の回数が増える、ということです。
検定を2回以上実施すると出てくる問題が、統計的検定の多重性の問題。
多重性の問題を考えると、1つの研究の中で、できるだけ検定を実施しないで解析する方針を取ることが重要です。
もう一つの問題は、得られているデータの数(サンプルサイズ)で検定結果が左右されてしまうということ。
つまり、検定結果が有意だからと言って、本当に正規分布かどうかはわからず、単にデータの数が多いだけかもしれない。
反対に、有意じゃなかったとして、データの数が少ないだけかもしれない。
そういった問題がありますよね。
正規性の検定を実施しないならどうやって正規性を判断する?
ではどうやってデータの正規性を判断するのか?ということが問題。
結論として、基本的には、ヒストグラムを描いて釣り鐘状になっているかを観察します。
経験的知見から「このデータは正規分布に従うはずだ」と思えば、正規分布として解析してもかまわないません。
つまり、正規性の検定を実施するのではなく、ちゃんと要約統計量やグラフで可視化することによってデータ全体の傾向を判断することが重要。
検定はP値一つで判断できるので便利なのはわかりますが、ちゃんとデータ全体を確認することが大事です。
>>正規性の検定は本当に必要?ヒストグラムとQQプロットで十分な理由
SPSSで正規性の検定を実施するならこの手順!

そうは言っても、何かしらの理由で正規性の検定を実施しなければならない場合があるかもしれません。
そんなとき、SPSSではどうやって正規性の検定をするのか、手順をお伝えします。
SPSSで正規性の検定を実施するデータを取り込む
今回のデータはSPSSでT検定を実施したする記事と同じデータを使います。
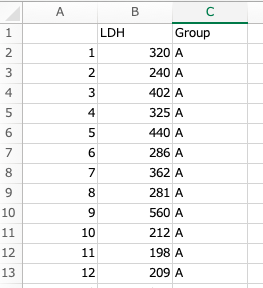
LDHが連続データで、Groupが群を示した変数です。
A群13例、B群11で、計24症例分のデータがあります。
このデータをを適切な場所に保存しておきましょう。
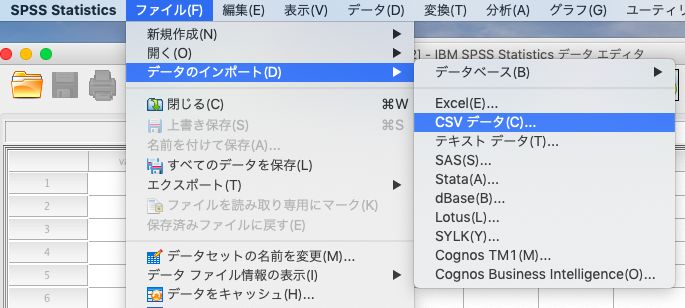
SPSSを開き「ファイル」→「データのインポート」→「CSVデータ」を選択します。
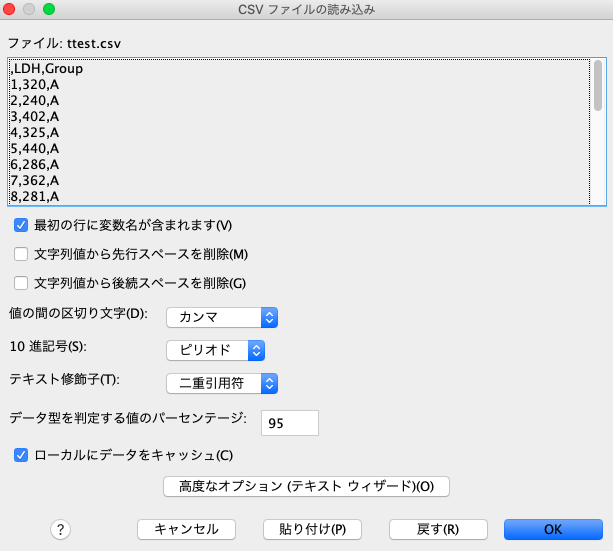
そうすると、以下のような画面になりますので、特にいじらずにOKで大丈夫です。
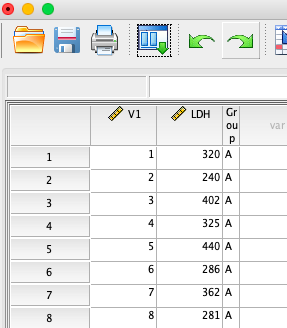
そうすると、以下のようにちゃんとインポートされました。
データの見た目は、エクセルと同じ感じですね。
連続量のデータであれば右揃えでデータが表示され、カテゴリカルデータであれば左揃えでデータが表示されます。
SPSSで正規性の検定を実施!
では実際に、SPSSで正規性の検定を実施してみます。
下図のように[分析(A)]→[記述統計(E)]→[探索的(E)]を選びます。
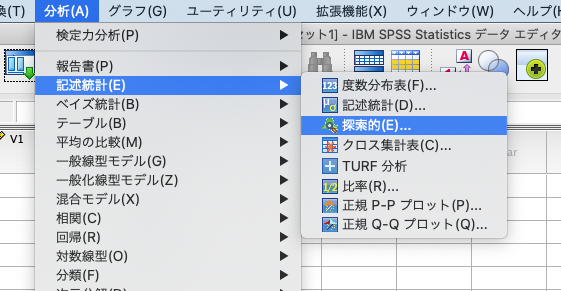
今回は、各群ごとにLDHの値が正規分布しているかどうかを確認しようと思います。
そのため、「従属変数」にはLDHを入れ、「因子」にGroupを入れます。
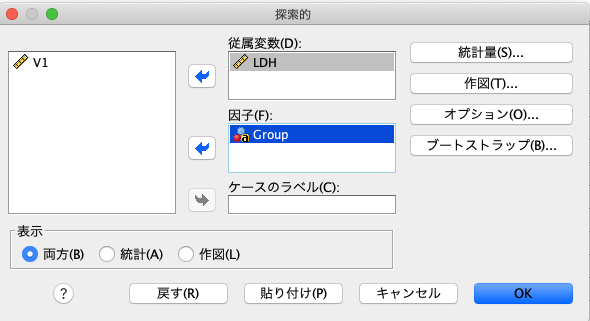
そして、「作図」をクリックして「ヒストグラム」にチェックを入れ、「正規性の検定とプロット」にもチェックを入れます。
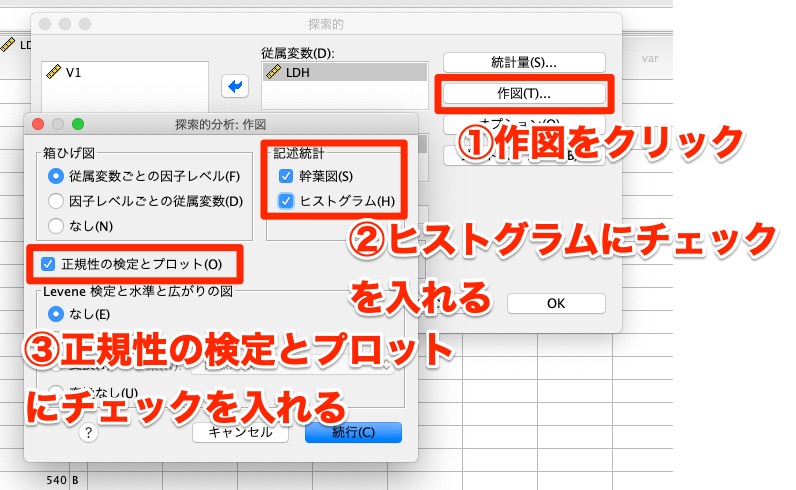
これで実行をすると、正規性の検定を実施することができます。
SPSSで実施した正規性の検定結果を解釈する
SPSSで色々と結果が出力されますが、まずは正規性の検定結果がどうなったのかを確認します。
下記の表が正規性の検定結果です。
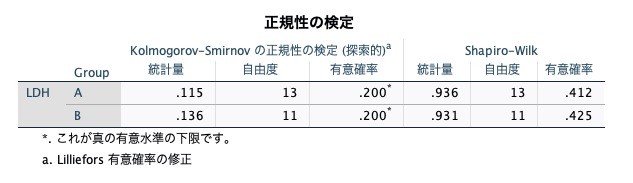
「Shapiro-Wilkの正規性の検定」と「Kolmogorov-Smirnovの正規性の検定」の二つが出てきています。
この二つの検定結果のどっちを見ればいいのか?という使い分けは、後ほど解説します。
今回のデータだと「Shapiro-Wilkの正規性の検定」の結果を見ればOK。
すると、有意確率(P値)が0.412と0.425なので、正規分布とみなしていいのでは、という判断ができます。
次に、ヒストグラムを確認してみましょう。
下図がGroupAに対するヒストグラム。
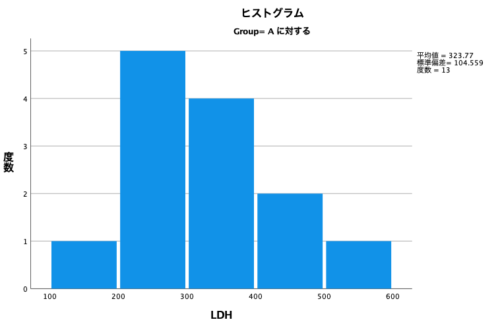
そして下図がGroupBに対するヒストグラム。
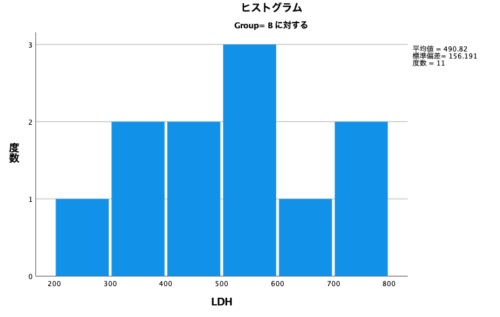
データが少ないのでなんともいえませんが、なんとなく正規分布っぽい形をしていますよね。
そして、QQプロットも出力されています。
以下がGroupAに対するQQプロット。
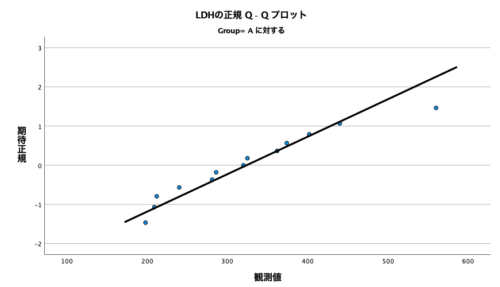
そして以下がGroupBに対するQQプロット。
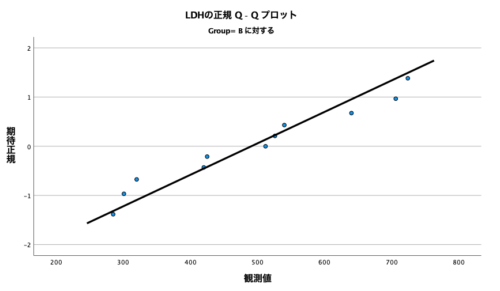
QQプロットの見方としては、とにかく直線関係があれば正規分布とみなせる、ということでした。
そのため、今回のQQプロットでは直線上にデータが集まっているように見えますので、ここからも正規分布と皆しても良いのでは、という判断ができます。
「Shapiro-Wilkの正規性の検定」と「Kolmogorov-Smirnovの正規性の検定」の使い分けは?
SPSSで正規性の検定が実施できたところで、最後の疑問。
「Shapiro-Wilkの正規性の検定」と「Kolmogorov-Smirnovの正規性の検定」の二つはどちらを信じればいいの?
ということです。
もう一度、SPSSで正規性の検定を実施した結果を示します。

「Shapiro-Wilkの正規性の検定」と「Kolmogorov-Smirnovの正規性の検定」の二つの結果、結構違いますよね。
なので、どちらの結果を採用するかは大事な問題。
この使い分けを検索してみると、SPSSのベンダーであるIBMのサポートサイトではこのように解説されています。
「Shapiro-Wilk」は5,000件以下のケースを分析すると自動的に追加され、それ以上のデータの場合は算出されない、正規性の検定手法です。
「Kolmogorov-Smirnov」と同様に、「変数は正規分布をしている」という仮説ですので、変数が有意水準未満であれば、「変数は正規分布をしていない」という結論になります。
「Shapiro-Wilk」は50件程度のデータに特化した手法になりますので、少ないケース数に対して正規性の検定を行う場合は、こちらをご提示してください。
引用:https://www.ibm.com/support/pages/kolmogorov-smirnov%E3%81%A8shapiro-wilk%E3%81%AE%E9%81%95%E3%81%84
そのため、少数データであれば「Shapiro-Wilkの正規性の検定」が良く、大規模なデータになると「Kolmogorov-Smirnovの正規性の検定」が良い、という使い分けになりますね。
SPSSで正規性の検定を実施する方法:まとめ

今回の記事では
- そもそも正規性の検定は必要なのか?
- 正規性の検定をSPSSではどうやって実施するのか?
- 「Shapiro-Wilkの正規性の検定」と「Kolmogorov-Smirnovの正規性の検定」の使い分けは?
ということをお伝えしました。
ぜひマスターしてくださいね!










コメント