近年、投稿論文の再現性の低さが研究上の大きな問題とされています。
再現性を確かなものとするために、様々な研究では統計学に基づいた解析が必要不可欠。
しかし、どんなに素晴らしい研究結果を得たとしても、統計的解析が間違っていては論文にすることはできません。
また、場合によっては統計的解析が間違いから、研究結果そのものの解釈が大きく変わることもあります。
とはいえ、“その統計手法が本当にあってるか?”を見分けるのは簡単ではありません。
そこで、この記事では、
- “投稿された論文でよくある10個の統計的間違い”
- “どうやって統計的間違いを見つけるのか?”
- “どうやって統計的間違いを解決するのか?”
についてわかりやすく説明していきます。
統計解析の重要性は、
>>>臨床試験(治験)で統計解析が必要な理由は?バイアス回避に重要
でも説明しています。
論文の統計の書き方で参考になる論文を紹介

本記事は、英国の神経科学者で、生命化学系のジャーナルeLIFE誌のReviewing editor のMakin氏が、“Ten common statistical mistakes to watch put for when writing or reviewing a manuscript”のタイトルで生命化学系のジャーナルeLIFEに2019年発表した記事を、日本語で要約したものです。
eLIFEはオープンジャーナル(閲覧料のかからない論文)なので、オリジナルの記事は以下のリンクから閲覧することができます。
https://elifesciences.org/articles/48175
論文でよく見られる10の統計学的な間違い

投稿された論文でよく見られる10の統計学的間違いは次のようなものがあります。
- 適切なコントロール条件/群がない
- 2つの効果を直接比較することなく個別の比較結果を解釈する
- 分析単位の膨張
- 偽りの相関
- 小さなサンプルの使用
- Circular分析
- 分析の柔軟性:P-ハッキング
- 多重比較の修正の失敗
- 有意でない結果の過剰解釈
- 相関と因果関係
これらの内容について詳しく見ていきましょう。
論文での統計的に間違った書き方その1: 適切なコントロール条件や群がない
どんなに正しい統計的操作を行って、統計的有意な結果を得たとしても、実験中に適切なコントロール条件/群が存在していなければ、統計的に有意なことは科学的な根拠とはなりません。
適切なコントロール条件や群がないことは統計的に何が問題か?
この問題は時系列で取られる実験データなどでよく見られます。
薬剤の効果など、何かの要素の効果を調べるときに、“複数の時間で測定を行う”ことは効果を評価するための科学の一般的な方法です。
しかし、研究対象となる要素以外の要因で、測定結果に変化が生じる可能性があり、特に時系列のデータでは他の要因の影響を受けやすいです。
例えば、同じ実験操作を繰り返すとき、実験者が操作に慣れるなど、目的となる影響以外の要因により測定結果に変化が生じることがあります。
このように、隠れた別の要因が測定結果に影響を与えている場合、実験の結果から導かれる結論に大きな誤りが含む時があります。
そのため、研究目的である要素のみの影響を明らかにするために、適切なコントロール条件/群を実験に含める必要があります。
また、見かけ上のコントロール条件/群が含まれているとしても、測定する値に影響を与える可能性がある要因が、考慮されていないこともあります。
適切なコントロール条件や群に関してどうやって解決するか?
適切なコントロール条件/群が存在するか、を念頭に実験計画を綿密に立てる必要があります。
理想的には実験条件は、”実験目的である要素”以外は、すべての条件がまったく同じことが望ましいです。
そのため、実験自体をコントロールと同時に行うなど、他の要因が結果に影響しないように工夫する必要があります。
そうすることで、ある要素のみの測定値への影響を明らかにすることができます。
もし、実験で他の要因による影響を取り除けない場合、考えられる他の要因からの影響を分離できないことを論文中に提示する必要があります。
論文での統計的に間違った書き方その2: 2つの効果を直接比較することなく個別の比較結果を解釈する
ある要素の影響を調査するときに、コントロール条件/群と直接には有意な影響はないのに、実験条件/群に有意な影響を与える別の結果から、ある要素の影響について結論をだすことがありますが、これは間違いです。
直接比較していないと何が問題か?
次のような実験を考えます。
それぞれ、20人からなるAとBのグループがあったとします。AとBのグループからそれぞれXとYという値を測定しました。
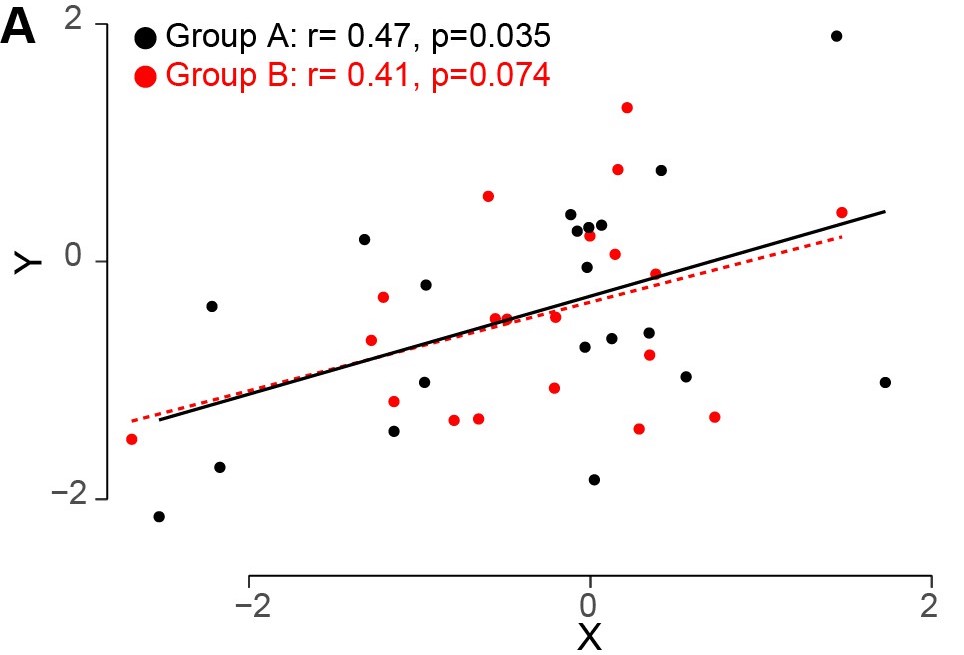
eLife 2019;8:e48175 よりFigure 1A
グループAではXとYには有意な相関(p< 0.05)があります。
>>>相関係数とは?p値や有意差をどう解釈すれば良いのかわかりやすく!
一方、グループBではXとYには有意な相関はありません。
このようなとき、“グループAはグループBよりも相関が大きい”と推論することは間違いです。
なぜなら、2つの変数間の関係が、2つのグループ間で全く同じ場合でも間違って有意性に差が起きてしまうからです。
2つグループについて別々の解析を行い、解析結果に基づいてどちらかのグループでの効果が、もう一方のグループ効果よりも大きいと、ときどき示唆されることがあります。
この間違いはよく行えあれますが、統計的には正しくありません。
直接比較の問題をどうやって発見するか?
この問題は、統計的に直接比較せずに、2つの効果の違いに関して結論が出されたときに起きています。
また、必要な統計分析を実行せずに、推論を行うあらゆる状況で発生する可能性があります。
直接比較の問題をどうやって解決するか?
グループを対比したい場合、グループを直接比較する必要があります。
2つの別々のテスト結果ではなく、直接一つの統計的解析を行うことが不可欠です。
グループ比較には、ANOVAが適しています。
>>>ANOVAとは?分散分析表の見方やf値とp値の意味もわかりやすく!
ノンパラメトリック統計はいくつかの方法がありますが、使用前に条件は適切かを十分に考える必要があります。
>>>パラメトリック検定とノンパラメトリック検定とは?例を使ってわかりやすく簡単に
論文での統計的に間違った書き方その3:サンプルサイズが大きすぎる
よくN数やサンプルサイズと呼ばれるものを、分析単位と呼びます。
例えば、あるグループにおける何らかの要素について推測する場合、分析単位はテストされた”被験者の数”です。
しかし、“観測の数”と”被験者の数”を混同がよく生じてしまってり、さまざまな問題をもたらします。
サンプルサイズが多いと何が問題か?
分析単位はサンプルサイズを意味します。
サンプルの数は、実験にもよりますが、研究計画の時点で自由に設定することができます。
統計では、分析単位は自由度に影響します。
しかし、分析単位を”サンプルの数”ではなく”観測数”と混合する間違いがよくみられます。
この間違いは、二つの問題をもたらします。
一つ目は、サンプル間に明確な識別がなければ、そもそも、適切な統計的評価ができません。
二つ目は分析単位の数を誤って多く見積もることになり、自由度が増加します。
自由度が増加すると、統計的有意性が判断される統計的しきい値が低くなるため、間違った統計的有意差が出ていますことがあります。
本来、有意ではないものが有意と間違って検出されることを、第一種の過誤と言います。
>>>αエラー(第一種の過誤)βエラー(第二種の過誤)とは?例やゴロで分かりやすく検出力との関係も
例えば、10人のグループを対象とし、別々の日に分けて、数種類の血圧を下げる薬を投与し、投与前後の血圧を測定したと考えてみます。
薬同士に相関があるかどうか調べるとしましょう。
分析単位は被験者の人数である10で、実際の自由度は8 です。
この時、有意に相関があるのに必要なR値は0.63です。
しかし、”測定の前”と”測定の後”を分けて考えないといけないという思いから、分析単位が間違って“観測数”とされることがあります
この時、投与前後の血圧から20個のデータがり、この時の自由度は18となります。
誤って自由度が大きくなると、統計的有意性が判断される統計的しきい値が低くなるため、有意に相関があるのに必要なR値は0.44となります。
もし実際のR値が0.63~0.44であったなら第一種の過誤が生じます。
サンプルサイズが大きいかどうかはどうやって発見するか?
血圧の例を考えましたが、ある薬の”摂取後の血圧”は”摂取前の血圧”とは切り離して考えることはできません。
このように、統計解析では、”サンプル内”ではなく”サンプル間”での違いを調べる必要があります。
そのため、測定を行う前に適切な分析単位が使われているか、を確認することが必要です。
サンプルサイズの大きさをどうやって解決するか?
投与前後の血圧というような、ある要素の効果を、操作の前後で”区別して解析したい”ときは、混合効果線形モデルを使用することが最善の解析手法です。
混合効果線形モデルでは、被験者内での変動を固定効果として定義し、被験者間の変動をランダム効果として定義できます。
しかし、高度な統計的理解が必要なので、注意して適用および解釈する必要があります。
もっとも簡単ないくつかの解析手法もあります。
一つ目は、各観測点の相関を個別に計算し、(例えば、薬の投与前と後の値の相関など)自由度に基づいて結果が有意かどうかを考えることができます。
次にある時点での観測値を平均化する方法があります。
あとは、相関を個別に計算し、結果のR値を平均化して解釈することもできます。
論文での統計的な間違いその4:偽りの相関(擬似相関)
相関は2つの変数間の関係性の大きさを評価するための、科学における重要なツールです。
ただし、ピアソン相関などのパラメトリックな相関はいくつかの仮定に基づいています。
そのため、仮定に該当しないときに、間違った相関を用いると、間違った相関が発生する可能性があります。
擬似相関は何が問題か?
ここでは2つの問題点を取り上げます。
一つ目はハズレ値の問題です。
下の図の上の行で●で示しているのが、ハズレ値です。
A,B,Cでは●以外はまったく同じところに○がありますが。ピアソン相関係数が異なっています。
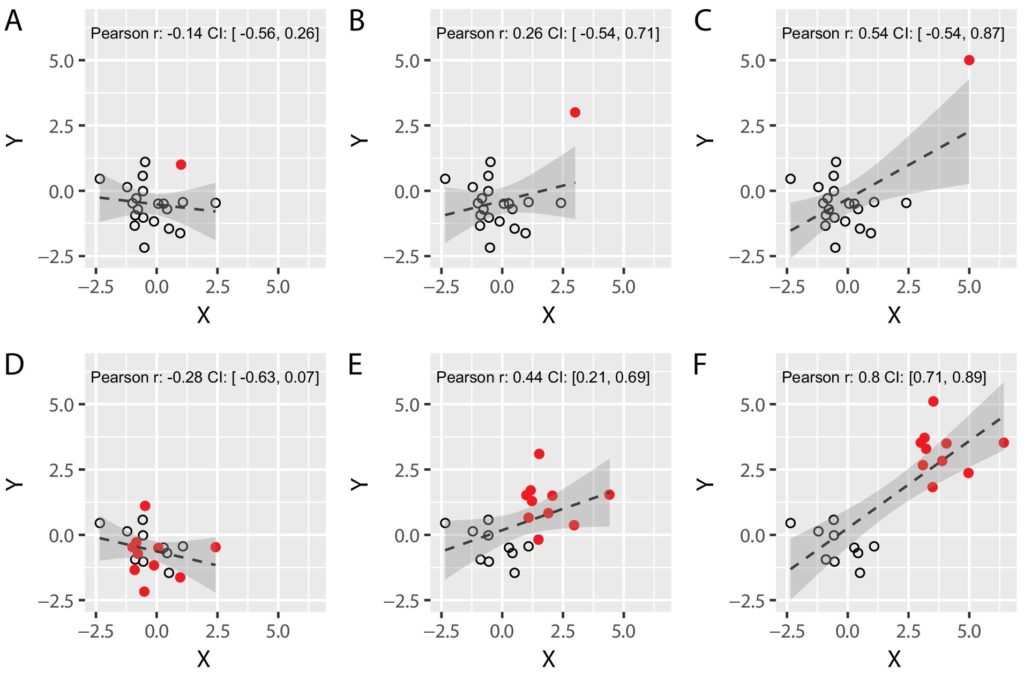
eLife 2019;8:e48175 よりFigure 2
このように、分布から大きく外れたバズレ値は、相関係数を大きく変化させることがあります。
しかし、ハズレ値自体もある現象の法則に従っている可能性があるため、不用意にハズレ値を取り除いてはいけません。
次にあるのが、2つのグループが混在することで相関が生まれる場合です。
上の図の下の行では●と○で表される2つのグループがあります。
EやFでは、●と○のそれぞれははっきりと分かれており、それぞれのグループ自体には正の相関はないですが、2つのグループが混在することで相関が生まれてしまいます。
擬似相関をどうやって発見するか?
散布図を伴わない相関に特に注意を払う必要があります。
また、ハズレ値を取り除いたときにバズレ値を取り除く正当な理由があるかを確認する必要があります。
複数のグループが一緒にされている可能性がある場合、グループ間または条件間の違いが考慮されているか考える必要があります。
擬似相関をどうやって解決するか?
ブートストラップ、データのウィンザー化、スキップされた相関などの堅牢な相関の算出法は、外れ値の影響を受けにくいため、ほとんどの状況で利用できます。
これらの相関の計算手法は、これらの手法がデータの構造を考慮に入れているため、外れ値の影響を受けにくくなっています。
パラメトリック統計を使用する場合は、データ間の独立性や外れ値の存在など、仮定に反していないか、実験データを確認する必要があります。
論文での統計的な間違いその5: 小さなサンプルサイズ
サンプルサイズが小さい場合、大きな効果しか統計解析では検出できません(有意差が出ません)。
実際の効果サイズの推定値に大きな不確実性が残り、実際の効果サイズが過大評価されます。
小さなサンプルサイズは何が問題か?
p値で0.05が有意性のしきい値として使用される統計解析では、すべての統計検定で5%が、第一種の過誤として知られる間違った有意な結果を出してしまいます。
>>>αエラー(第一種の過誤)βエラー(第二種の過誤)とは?例やゴロで分かりやすく検出力との関係も
高い相関係数( R> 0.5など)を持つ場合、弱い相関( R = 0.2など)を持つときよりも、“結果は確実”である、
つまり、より高い相関係数の方が結果が正しい、と誤って解釈されてしまいます。
しかし実際には、相関係数の大小などの値に関わらず、間違って有意になっている可能性があります。
特に、サンプルサイズが小さいと、
誤検知の可能性が大きくなり、有意性に誤りが起りやすくなります。
そのため、
「サンプルサイズが小さくて、誤検知の影響サイズが大きとき、統計の結果は有意にしかならない」
という重大な誤りが生じることもあります。
サンプルサイズが小さい解析では、データに存在する効果を見逃しやすくなります(第二種のエラーまたは偽陰性)。
より大きなサンプルサイズを用いると、統計によって実施の効果を適切に検出する可能性が高くなります。
この可能性の大きさのことを”統計的検出力”と呼びます。
したがって、大きなサンプルを使用すると、第二種の過誤の可能性が低くなります。
サンプルサイズが小さいことには別の問題もあります。
小さいサンプルサイズでは、サンプルの分布が正規性から逸脱する可能性が高く、サンプルサイズが限られているために、正規分布の仮定をおく検定において、厳密にテストすることが不可能になることがあります。
小さなサンプルサイズはどうやって発見するか?
論文で使用されているサンプルサイズを厳密に調べ、サンプルサイズが十分かどうかを判断する必要があります。
限られた数のサンプルに基いた考察を行う時は、第一種の過誤や第二種の過誤などの懸念について、注意事項を論文中に書く必要があります。
小さなサンプルサイズをどうやって解決するか?
小さなサンプルから得られるp値は限られた意味しか持ちません。
実験前に、使用する統計解析の検出力を提示などして、最初に効果を検出するのに十分な能力があるという証拠を提示するか、別の実験により再現性を確認する必要があります。
特に、難病など限られた臨床集団を調べるとき、サンプルのサイズが必然的に限られる時があります。
サンプルのサイズが必然的に限られる時は、そのサンプル数での信頼区間を算出するなどして、どのくらいの精度で議論できているかを、論文中で説明をする必要があります。
論文での統計的な間違いその6:Circular分析
Circular分析は、データの特徴に基づいて母集団を加工する、分析方法です。
しかし、間違ったCircular分析はでは、都合の良い結果を得るために、実験データを解析後に、都合よく加工するようなときに生じます。
Circular分析は何が問題か?
Circular分析は、ときに統計的テストの結果に誤りをもたらします。
最も一般的には、Circular分析は、元のデータセットを何かの特徴によって、母集団を分割(例えば、サブグループ化など)または、縮小(例:関心領域の定義、「外れ値」の削除)することです。
例として、
ある操作に応じたニューロン集団発火率の研究を考えます。
ニューロンの母集団全体を比較すると、操作前と操作後の間に有意差は見られません。
しかし、発火率を上げることで操作に反応するニューロンもあれば、操作に反応して減少するニューロンもあることを以前に観察していたとします。
そこで、操作前のニューロンの活動レベルに基づいて、母集団をサブグループに分割しました。
これにより、次の実験結果が得られました。
「最初に低反応を示したニューロンは反応の増加を示し、
最初に比較的増加した活性を示したニューロンは操作後に減少した活性を示す。」
ただし、この実験結果は間違っています。
それは。正しくない選択基準による母集団のサブグループ化により、ノイズの影響によってもたらされたもので、実際の効果ではないからです。
間違ったCircular分析が生じるのもう1つ原因は、従属変数と独立変数の間に依存関係が作成される場合です。
先ほどのニューロンの例を続けると、操作後の細胞反応と、操作前の細胞反応の違いについて相関を用いてを考察を行うかもしれません。
しかし、操作後の細胞反応と、操作前の細胞反応は操作後の測定値に大きく依存しています。
したがって、操作後の測定で偶然により強く発火するニューロンは、操作前の測定に比べて大きな変化を示す可能性が高くなり、相関が大きくなります。
データを加工した後の解析結果が、
データを加工したことと統計的に独立していることを示せた場合、
データを加工することは間違っていません。
データの加工によってのみで得られる結果は、実験のノイズが間違って特徴付けられることで、統計的推論が科学的に意味をなさなくなります。
Circular分析の間違いをどうやって発見するか?
間違ったCircular分析は多く場面で現れますが、
原則として、仮説を支持する結果を得たいときに、加工されたデータによる統計的検定が行われることで、よく発生します。
たとえば、研究対象の効果が、加工だれたデータの統計解析に基づいている場合によく出現します。
他の状況では、データの加工により分析が複雑になり、データの加工の統計への影響の理解が難しくになる場合に生じます。
複雑なデータの加工は理論的に妥当ではない可能性があります。また加工が行われているデータは、比較的信頼できない測定値に基づいている可能性があります。
そのため、
データをどのような基準に基づいて加工をしたか、が適切に記述されていること。
また、データの加工と研究目的の効果に、独立性の証明がされていること。
この二つを確かめるべきです。
Circular分析をどうやって解決するか?
解析をする前に、
独立して分析基準をあらかじめ定義することで、
誤ったCircular分析に陥りにくくなります。
Circular分析はノイズを間違って解析することで、分析結果を歪めることがあるため、ノイズの様子が異なる別のデータセットを使用することで、解析が間違ってないかを確認することもできます
必要に応じて、ブートストラップなどのシミュレーションを実行して、研究結果がノイズや選択基準とは関係ないことを示すこともできます。
論文での統計的な間違いその7:分析の柔軟性:P-ハッキング
有意差が出るp値になるまで、実験データを加工しては検定を行う作業を続けることを、P-ハッキングと呼んだりします。
>>>T検定とは?帰無仮説と対立仮説を必ず確認!F検定で等分散の確認が必要?
P-ハッキングは何が問題か?
データ分析を柔軟性を持って加工し、有意性が認められるまで
結果パラメーターを変えたり、共変量の追加したり、確立していない前処理をし、実験後にハズレ値を決めたりなど、
検定をたくさんを行うと、いつかは有意性が出ます。
これは、統計手法が確率に依存しているため、実行する検定が多いほど、第一種の過誤が発生する可能性が高くなるためです。
>>>αエラー(第一種の過誤)βエラー(第二種の過誤)とは?例やゴロで分かりやすく検出力との関係も
p値を計算することは、研究対象の効果を解析する際に非常に強いツールとなります。
しかし、分析手法が複雑になるほど有意性が出た効果が第一種の過誤である可能性が高くなります。
特に、この問題は同じ研究室が同じ結果変数を報告するとき、論文全体で異なった検定方法でp値を計算する場合に特に顕著に見られます。
P-ハッキングを防止する最善の方法は、p値と有意差にこだわりすぎないことです。
有意差が出そうなp値の境界線(p=0.053とか)、または有意ではない結果に対してそうするべきです。
言い換えれば、実験がうまく設計され、実行され、分析されている場合、データを責める必要はありません。
P-ハッキングをどうやって発見するか?
論文では、分析の柔軟性を検出するために必要な情報を、すべて公開することはめったにないため、この問題を検出することは困難です。
事前登録または臨床試験登録の場合、実行された分析を計画された分析と比較する必要があります。
事前登録がない場合、いくつかの形式のpハッキングを検出することはほとんど不可能です。
P-ハッキングはどうやって解決するか?
結果の報告において透明性を保つ必要があります。
たとえば、事前に計画された分析方法と、予測された結果、予想外の結果を区別する必要があります。
つまり、実際に行った方法を正直に記載し、
もし、p値が有意水準にならなかったとしても、そのことを認めて論文に記載するべきです。
論文での統計的な間違いその8:多重比較の修正の失敗
3つ以上の条件(または2つのグループの比較)を含む実験デザインでは、
統計解析を行う場合、複数の比較が含まれ偽陽性を検出する確率が高くなります。
>>>多重性とは?その意味と統計検定のp値を解釈する上で重要なこと
多重生の修正の失敗は何が問題か?
3つ以上の条件を含む実験では、複数の比較が含まれ、実際に効果が存在しない場合でも、第一種の過誤として間違った結果を得る確率が高くなります。
この場合、行う検定の数が多いほど第一種の過誤が生じる確率が増加します。
たとえば、
2×3×3の組み合わせがある実験計画では、
どんなに効果がない場合でも、少なくとも1つの重要な主効果または相互作用効果を間違って見つける確率は30%です。
この問題は、複数の独立した比較を行うときに特に顕著に起ります。
多重生の問題をどうやって発見するか?
この問題は、測定された独立変数の数と実行された検定の数を確認することで発見できます。
複数ある変数のうち1つのみが従属変数と相関している場合、重要な結果を得る可能性を高めるために、残りが含まれている可能性があります。
したがって、多数の変数(例えば、遺伝子発現解析など)を使用して、探索的分析を実行する場合、
“明確な正当化なしに、多重比較の補正によって有意とならなかった結果を検定から解釈する”
ことはあってはいけません。
多重生の問題をどうやって解決するか?
測定されたすべての変数を開示し、多重比較手順を適切に説明する必要があります。
多重比較を修正するには多くの方法があります。
>>>多重性の調整方法は?統計学的検定の多重性を補正する3つの方法
論文での統計的な間違いその9:有意でない結果の過剰解釈
結果が有意でないに統計的検定の結果を誤って解釈することは問題ですが、一般的起こっている間違いです。
例えば、統計的有意差がないからといって、効果はないとは言えません。
有意でない結果の過剰解釈が何が問題か?
統計を使用する場合、統計的有意性を判断するために統計的しきい値、通常はp値0.05を適用します。
しかし、結果が有意でない場合に、統計的検定の結果を誤って解釈することがしばしば見受けられます。
これは、有意ではないp値は、実際に影響があるかどうかと、サンプル数に依存した検出力の大小を区別していないからです。
有意でない結果の過剰解釈をどうやって発見するか?
効果が存在しないことを示すものとして、有意でないp値を提示したとき、これは間違いです。
有意でない結果の過剰解釈をどうやって解決するか?
研究対象となる効果の大きさに関する情報を提供するために、実測値をp値とともに報告することが必要です。
どうしても、効果がないことを示す場合、有意にならなかった証拠と帰無仮説をサポートする証拠を区別できる統計的アプローチをを検討する必要があります。
あるいは、目的の効果を特定するのに十分な統計力があるかどうか、実験計画の時点で考慮することもできます。
それ以外の場合、有意ではないを過度に解釈せず、有意ではないものとしてのみ説明する必要があります。
論文での統計的な間違いその10:相関と因果関係
相関関係と因果関係を間違えてはいけません。
相関と因果関係の間違いは何が問題か?
相関関係と因果関係を混合することは、統計結果を解釈するときに行われる最も古く、最も一般的なエラーです。
科学では、2つの変数間の関係を調べるために相関関係がよく使用されます。
2つの変数が有意に相関していることがわかった場合、一方の変数が他方の変数の変化を引き起こしていると仮説立てることがよく行われます。
ただし、これは正しくありません。
2つの変数間に線形の関係しているように見えるからといって、
たとえ、そのような関連性がもっともらしい場合でも、必ずしもそれらの間に因果関係があることを意味するわけではありません
たとえば、
さまざまな国の年間チョコレート消費量とノーベル賞受賞者数との間に有意な相関が観察されました。
これによりチョコレートの摂取が、ノーベル賞受賞者を生み出すための栄養的根拠という(誤った)報告も存在します。
相関関係だけを、因果関係の証拠として使用することはできません。
相関は、直接または逆の因果関係を反映する場合がありますが、共通の原因による場合もあり、単純な偶然の結果である場合もあります。
相関と因果関係の間違いをどうやって発見するか?
2つ以上の変数間の相関関係を報告し、因果関係のについての議論を行う場合は常に、相関関係と因果関係が混乱する可能性があります。
変数が実際に実験で操作できている場合にのみ因果関係の議論を行うべきであり、
その場合でも、第3の変数または交絡因子の役割に注意する必要があります。
相関と因果関係の間違いをどうやって解決するか?
可能であれば、競合モデルをテストするか、変数を直接操作するなどして、第3の変数との関係を調べて解釈をさらに深めるがあります。
それが難しく、証拠が相関関係しかない場合、因果的な考察は避けられるべきです。
まとめ
統計的な失敗の多くは、綿密な実験計画が建てられていないことに起因します。
そのため、研究には綿密な実験計画が欠かせません。
また、実験結果や実験内容には正直である必要があり、実際にやったことを正確に論文に記述することが大切です。
たとえ、統計解析が間違っていたとしても、実際にやったことを正確に論文に記述されていれば、研究者として責められることはありません。
この記事では10の統計解析でよく見られる間違いをまとめました。
この記事が統計解析を行う上で、少しでも助けになれば幸いです。














コメント