傾向検定とは？初心者にもわかるトレンド検定の基本と使い方

「年齢が上がるほど病気のリスクが高まる」

「広告の表示回数が増えると購入率も上がる」

こうした“傾向”は直感的に理解しやすいですが、果たして本当にそう言えるのでしょうか？

目の前にあるデータに一貫した変化があるのかを確かめる方法が、傾向検定（トレンド検定）です。

統計の世界では、ただ「違いがあるか」ではなく、「順序に沿って変化しているか」を確認することがとても重要な場合があります。マーケティング分析から医療・社会調査まで、傾向検定はあらゆる分野で活用されています。

この記事では、統計初心者の方でも理解できるように、

• 傾向検定とは何か？
• どんな場面で使うのか？
• 主要な手法と使い分け
• 実際のデータを使った分析例
• 多変量解析への応用方法

などを、具体的な図表や事例を交えてわかりやすく解説していきます。

データの“流れ”を見逃さない分析スキルを身につけたい方は、ぜひ最後までご覧ください。

傾向検定（トレンド検定）とは？

傾向検定（トレンド検定）とは、ある順序に従ったカテゴリカル変数において、何らかの結果がその順序に沿って増加または減少しているかを統計的に検証する方法です。

たとえば「年齢が上がるにつれて高血圧の割合が増えているか」「所得階層が高いほど購入率が高いか」など、データの“流れ”や“方向性”を確認したいときに用いられます。

通常の比較検定（たとえば2群間のt検定やカイ二乗検定）は、グループ間に差があるかを検証します。一方で、傾向検定は「順序に沿った一貫したパターンがあるか？」に着目するのが特徴です。

傾向を検定するってどういうこと？

ここでいう「傾向」とは、順序があるカテゴリ（順序尺度）に沿って、結果が単調に変化している状態を意味します。

たとえば次のようなデータがあったとします。

年齢層	喫煙率
20-29歳	10%
30-39歳	15%
40-49歳	20%
50-59歳	25%

このように年齢層が上がるにつれて喫煙率も上昇している場合、「上昇傾向がある」と判断できます。

ただし、この判断はあくまで見た目であり、サンプル数が少ない場合などには偶然による変動の可能性も否定できません。

そこで統計的に「この傾向が偶然ではない」と裏付けるために、傾向検定を行うのです。

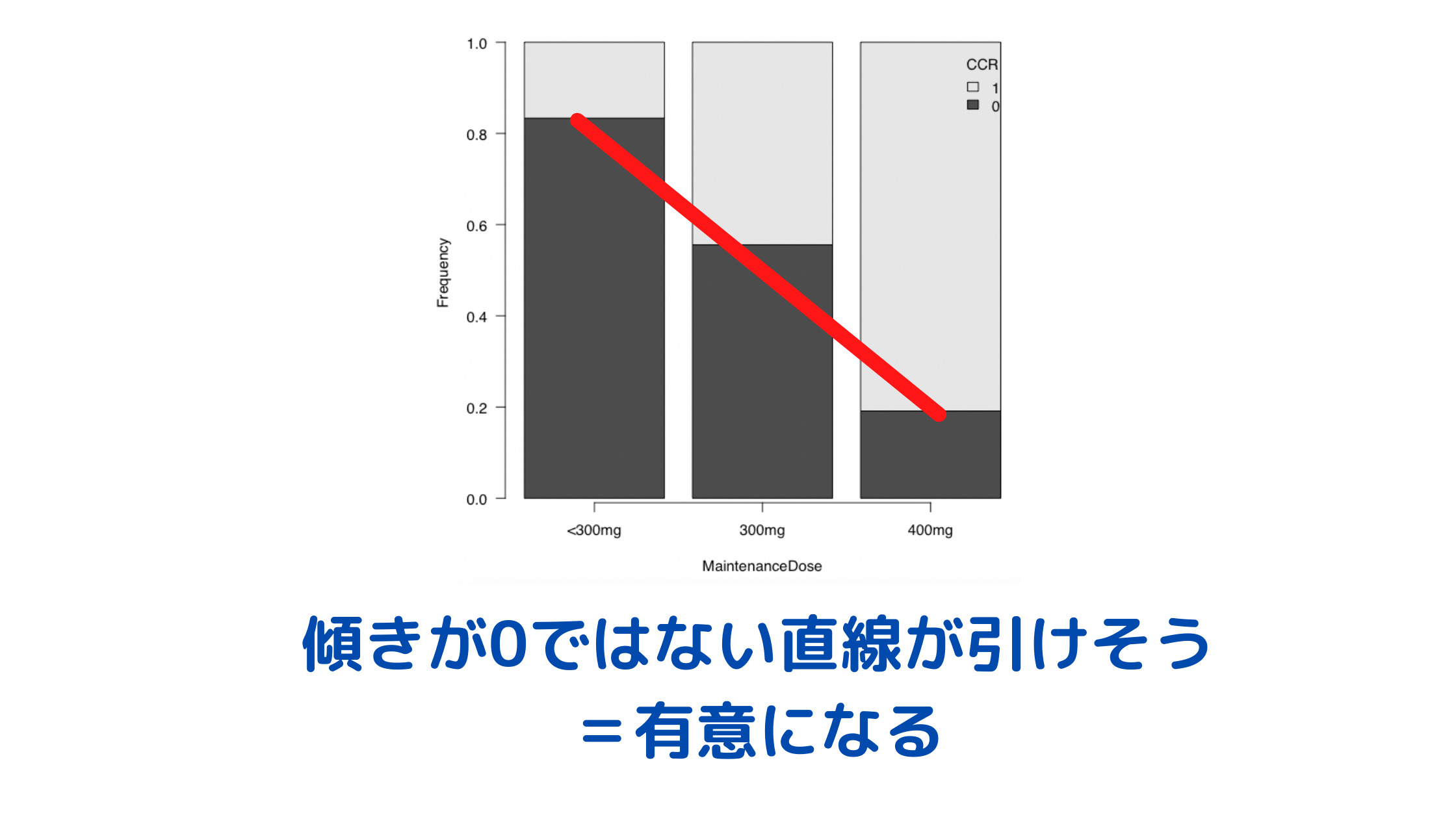
傾向検定の一般的な適用例とその意義

傾向検定は、さまざまな分野で活用されています。以下はその一例です。

• 医療分野：治療群の投与量に応じた改善効果の傾向を検証（例：プラセボ、低用量、高用量）
• マーケティング：接触頻度と購買意欲の関係を評価（例：広告表示1回、3回、5回）
• 社会調査：所得水準と満足度の関係性を探る（例：低所得、中所得、高所得）

このように、傾向検定は「ただの差」ではなく、「方向性のある変化」を明らかにしたい場面で非常に有効です。視覚的に見える傾向を、統計的に確かな裏付けに変える力があるのです。

傾向検定が必要となるシーンとは？

傾向検定は、さまざまな場面で適用することができます。

傾向検定が使える場面1：社会調査やアンケートにおける活用

傾向検定は、アンケートや意識調査などの社会調査において非常に重要な分析手法のひとつです。

たとえば、「年齢が上がるにつれて、政府に対する信頼度が変化しているかどうか」を検証するケース。

年齢を20代、30代、40代…と順序のあるカテゴリに分類し、それぞれの信頼度（高い・普通・低いなど）との関連性を調べる際に、傾向検定を使えば「一貫した増加または減少」があるかどうかが判断できます。

このように、年齢・収入・学歴など順序性を持つ変数を軸にした分析では、単なるクロス集計だけでは見えてこない「方向性ある違い」が明確になります。

傾向検定が使える場面2：医療・臨床研究での活用

医療分野では、傾向検定は非常に重宝されています。

特に、薬剤の投与量と治療効果の関係を検討する臨床試験では頻繁に用いられます。

たとえば、3つのグループ（プラセボ・低用量・高用量）における副作用発生率を比較する際、単なる有無ではなく「用量が増えるほど副作用が多い」といった明確なトレンドがあるかを確認する場面もあります。

このようなケースで傾向検定を使うことで、治療方針の意思決定や薬剤の安全性評価に説得力を持たせることができます。

傾向検定が使える場面3：マーケティング分析での使い方

マーケティング分野でも、傾向検定は有効です。

たとえば、広告の表示回数が増えると、商品の購入率がどう変化するのかを検討する場合、表示回数（1回、3回、5回…）と購入率の関係にトレンドがあるかを検定します。

この結果を元に、「何回の広告接触で購買意欲が最も高まるのか」「逆に接触しすぎて効果が下がっていないか」といった戦略的判断に活用されます。

また、A/Bテストなどの実験分析においても、「施策レベルごとに反応率が上がっているか」を調べる際に、傾向検定が役立ちます。

傾向検定は実務での“気づき”を可視化する力

傾向検定は、「なんとなくそう見える」を「データでそう言える」に変える手段です。

特に実務では、データを使って説得力のある説明をしたい場面が多くあります。たとえば：

• 「営業回数が増えれば、受注率も上がるのか？」
• 「製品レビューの評価点が新モデルで一貫して高くなっているか？」

こうした問いに対し、傾向検定は明確な方向性をもって答えを導く力を持っています。

傾向検定の主要な手法とその違い

傾向検定にはさまざまな手法がありますので、その違いを理解しましょう。

Cochran-Armitage検定とは？

Cochran-Armitage検定（コクラン・アーミテージ傾向検定）は、傾向検定の中でも最もよく使われる方法の一つです。

主に2×kのクロス表（例：ある事象の有無 × 順序付きカテゴリ）を扱うときに適用されます。

たとえば、「喫煙の有無」と「年齢層（20代・30代・40代…）」というように、順序のあるカテゴリ変数における割合の傾向を検定する際に有効です。

この検定の特徴は、各カテゴリに順序スコア（1,2,3など）を割り振ることで、結果の変化が直線的な傾向を持つかどうかを評価できる点です。

よくある疑問として、「カイ二乗検定とどう違うの？」という声があります。結論から言えば、目的が違います。

• カイ二乗検定：グループ間に「差があるか」全体的に見る
• 傾向検定（Cochran-Armitageなど）：「順序に沿った傾きがあるか」見る

つまり、傾向検定はカイ二乗検定の一種でもあり、より絞り込んだ視点での検定と捉えるとわかりやすいです。

たとえば、カイ二乗では差があっても、傾向検定では「その差が一貫して増加傾向にあるかどうか」まで見極められます。

Jonckheere-Terpstra検定の特徴

Jonckheere-Terpstra検定は、3群以上の順序付き群における連続データ（スコアなど）の傾向を検証する非パラメトリック検定です。

例えば、「患者の重症度（軽・中・重）によって血圧が上昇するか？」のように、順序グループごとのスコアに単調な変化があるかを検定できます。

この検定は、正規分布を仮定しないため、実データに適応しやすいのが強みです。

ノンパラメトリックながらも、順序の情報を活かした分析が可能です。

3-4. 傾向検定を選ぶ際のポイント

傾向検定の手法を選ぶ際には、以下のポイントをチェックしましょう：

チェック項目	適した検定手法
目的変数が2値のカテゴリ＋説明変数が順序あるカテゴリ	Cochran-Armitage検定
目的変数がが連続値＋説明変数が順序あるカテゴリ	Jonckheere-Terpstra検定
単なる差の有無を確認したい	カイ二乗検定またはANOVA
多変量要因も調整したい	ロジスティック回帰や順序ロジスティック回帰（後述）

検定手法は、目的・データの性質・順序性の有無によって最適なものを選ぶ必要があります。

目的を明確にすることで、結果の信頼性も大きく向上します。

多変量解析でも傾向検定はできる？

これまで紹介した傾向検定（Cochran-Armitage検定など）は、基本的に単変量の分析、つまり「ある1つの要因の順序に沿って、結果がどう変化するか」を見る方法です。

しかし、実際のデータ分析では「他の要因の影響も加味したい」という場面が多くあります。

たとえば、「年齢が上がるほど病気の発症率が上がっている」と見えたとしても、実はそれは喫煙習慣や性別など他の因子の影響かもしれません。

このように、交絡因子の存在があると、単純な傾向検定だけでは「真の傾向」を正しく捉えきれない場合があります。
そこで出てくるのが、多変量解析との組み合わせです。

では、多変量解析で傾向検定ができるのかと言えば、「限定的にはできる」ということになります。

ロジスティック回帰や共分散分析でトレンドを見る方法

たとえば、従属変数が2値（はい／いいえ）の場合に使われるのがロジスティック回帰分析です。

ここで、順序性のあるカテゴリ（例：運動習慣の頻度＝低・中・高）を数値（1, 2, 3）に変換してロジスティック回帰に組み込むと、「運動頻度が高くなるほど健康状態が良好になるか」といったトレンド（傾向）を評価することが可能になります。

また、他の変数（年齢・性別・収入など）を同時に含めることで、交絡因子を統制した上での傾向検定ができます。

このように、多変量解析で傾向を見る際には、順序カテゴリ変数を数値化して投入する必要があります。

ただし、その数値化には注意が必要です。単純に「1, 2, 3」として扱うことで、等間隔を前提にしてしまうリスクがあるからです。

また、変数が実際には順序的ではない（実はカテゴリごとに意味が異なるなど）場合は、誤った傾向の解釈につながる可能性もあるため、データの意味づけと検定の前提をよく確認することが大切です。

層別Cochran-Armitage検定（Stratified Trend Test）

複数の交絡因子によって層別されたデータに対して、各層ごとの傾向検定を実施し、それらを統合するアプローチです。

実務上は、「年齢層ごとの傾向を見るが、性別も交絡因子として考慮したい」などのケースで使われます。

Mantel-Haenszel型の統合方法を用いて、層別された傾向スコアの合計を統計的に評価することができます。

たとえば Rの coin パッケージを用いることで、このような解析ができます。

傾向検定の結果の読み方と注意点

傾向検定のp値と有意性の解釈

傾向検定の結果を見る上で、まず注目すべきはp値（有意確率）です。

一般的に、p値が0.05未満（5％未満）であれば、「統計的に有意な傾向がある」と判断されます。

たとえば、「広告表示回数が多くなるにつれて購入率が上昇している」ときに、p = 0.03 という結果が出れば、

✅「この傾向は偶然ではなく、広告表示回数と購入率の間に一貫した増加傾向がある」と言える

ということになります。

一方で、p値が0.1（10％）など比較的大きい場合は、「統計的に傾向があるとは言えない」という判断になります。

ただし、実務では“傾向はありそう”と感じるものの有意ではないことも多いため、p値だけで機械的に判断せず、結果の意味や実務への影響も考慮することが大切です。

傾向検定では事前にサンプルサイズ計算をしておらず、他の検定との多重性の問題に対して調整が入ることはないと思いますので、あくまで名目上のp値です。

結果の解釈は、単なる「有意/有意じゃない」という二元論で結論づけられるものではないことを意識しましょう。

傾向検定で有意差が出たとき・出なかったときの考え方

有意差が出た場合は、「順序性に沿った一定の変化が見られる」と統計的にある程度裏付けられた状態です。

この結果は、レポートや報告書で明確な根拠として使えるため、意思決定の根拠になります。

一方で、有意差が出なかった場合でも、「傾向が存在しない」と断定してはいけません。

なぜなら、以下のような要因が影響していることがあるからです：

• サンプルサイズが小さく、検出力が不足している
• データのばらつきが大きい
• 順序性のスコア付けが適切でない
• 傾向が非線形（単調でない）な可能性がある

したがって、p値が有意でも有意でなくても、「検定手法やデータの構造を再確認する」姿勢が求められます。

まとめ：傾向検定は“データの流れ”を捉える強力なツール

ここまで、傾向検定（トレンド検定）の基本から応用までを紹介してきました。

改めてポイントを整理すると、傾向検定とは：

• 順序性を持つカテゴリ変数に沿って、ある結果が単調に変化しているかを調べる統計手法であり、
• 単なる差ではなく、方向性のある「流れ（トレンド）」の有無を明らかにすることができます。

代表的な手法には、以下のようなものがあります。

検定名	特徴
Cochran-Armitage検定	2×kのカテゴリで比率の傾向を評価
Jonckheere-Terpstra検定	順序付き群における連続データの単調な変化を検定
ロジスティック回帰分析	他の変数を調整しながら傾向を検討可能

これらの手法は、医療・マーケティング・社会調査など多くの現場で活用されており、仮説検証や施策評価に欠かせないツールとなっています。

もしあなたが「データをもっと活かしたい」「説得力のある分析をしたい」と考えているなら、傾向検定は必ず知っておくべき技術です。

難しそうに見えても、考え方はシンプル。まずは「順序があるカテゴリ」に注目し、「その順序に沿って結果が変わっているか？」という問いを持つことから始めてみてください。

そして、自分の分析や報告の場面に合わせて、適切な手法を選べるようになれば、あなたのデータ分析スキルは確実に一段階アップするはずです。